Shortcomings of Simple EMC Filters

Oversimplification of EMC filter selection to reduce size and cost can often be a false economy as anticipated performance may not be achieved.

INTRODUCTION

EMC design principles are best considered at the equipment design stage, where good mechanical design including component layout and cable routing can help reduce EMC problems at source. Even with good EMC practice, it is invariably necessary to provide a certain amount of filtering. Cost and size considerations will usually encourage the use of a simple filter design. This can sometimes be a false economy as simple designs may not always give expected results. This can have serious compliance implications if EMC specifications have to be met. Some of the commonly encountered problem areas and their solutions are discussed in this article.

PROBLEMS & SOLUTIONS

When using suppression capacitors either on their own or in filters, it is most important to keep lead lengths as short as possible. An ideal capacitor of capacitance value C would have a linear impedance characteristic Z expressed by Z=1 / 2πfC, where f is the measurement frequency.

However, a real two-terminal capacitor will resonate at a frequency determined by its capacitance and the inductance L of its leads. The resonant frequency is given by f=1 / 2π √ LC. Below the resonant frequency, the capacitor impedance follows the ideal response, but, above the resonant frequency, the capacitor suppression performance reduces dramatically. Increasing the lead length reduces the resonant frequency and causes a loss in performance of the capacitor.

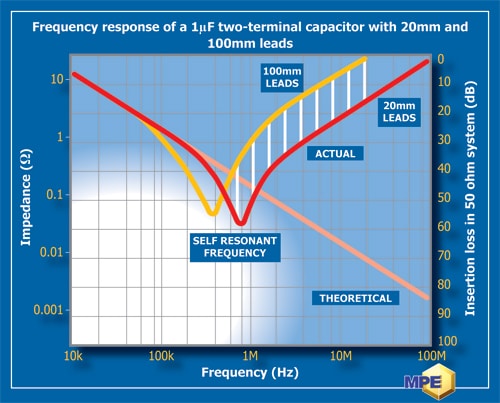
This can be seen in Figure 1, which compares the impedance of a 1μF capacitor with 20mm and 100mm leads. The leads of a two-terminal capacitor will typically have an inductance of about 7nH per 10mm lead length, which gives a resonant frequency of about 800kHz for a 1μF capacitor with 20mm leads. The shaded area on the graph indicates the loss in performance caused by increasing the lead length from 20mm to 100mm.

Above its resonant frequency, the two-terminal capacitor behaves as an inductor with the inductance L of its lead wires. Its impedance then becomes Z=2πfL. If suppression performance is needed above the resonant frequency in line-to-earth applications, then a feedthrough capacitor must be used. Apart from a few minor resonances related to the dimensions of the capacitor element, the feedthrough capacitor has a performance close to the ideal.

Figure 2 shows the physical differences between two-terminal capacitors and feedthrough capacitors. Figure 3 compares the performance of a 1μF feedthrough capacitor with a 1μF two-terminal capacitor. The shaded area shows the significant filtering performance not attainable from a two-terminal capacitor, which can be achieved by using a feedthrough capacitor of the same value.

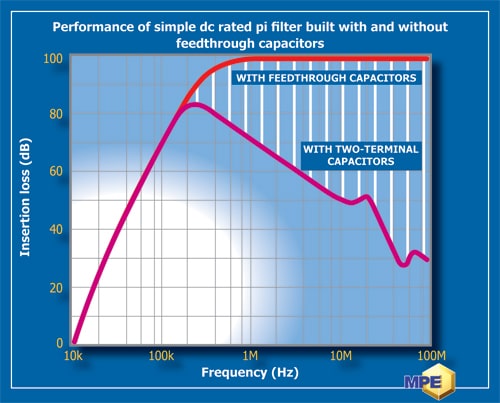
For the same reason, good high-frequency performance in filters can only be obtained if the filter incorporates feedthrough capacitors. As an example, Figure 4 shows the insertion loss performance of a simple DC pi filter built with feedthrough capacitors, compared to the same filter built with two-terminal capacitors. The shaded area indicates the extra performance obtained by using feedthrough capacitors in the filter design. Note that this graph is displaying insertion loss as opposed to impedance on previous graphs so is plotted in the more usual direction for insertion loss.

Many older EMC specifications specify equipment emissions and susceptibility requirements only up to 30MHz, and usually a filter containing two-terminal capacitors will be adequate to comply with these specification requirements. Newer specifications are now demanding EMC compliance up to 1GHz or beyond. This is to provide some protection against the effects of increased high-frequency noise pollution generated by faster processors, mobile phones, faster power control switches and so on.

The user should be aware that, even if his equipment has a CE mark to demonstrate compliance with existing EMC specifications, he could still experience problems. Unless his equipment is fitted with a suitable high-frequency filter containing feedthrough capacitors, it is unlikely to be protected against incident high-frequency interference above 30MHz. He could still therefore be responsible for problems caused by his equipment malfunctioning as a result of susceptibility to high-frequency interference.

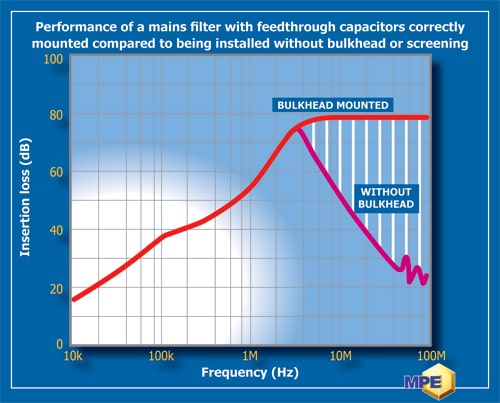
Even when using feedthrough capacitors, performance can be compromised if the filter or capacitor is not mounted correctly to suitably screen the input from the output terminals. Bypass coupling owing to radiation and pick-up on interconnecting wires is more pronounced at higher frequencies, so greater care is needed to avoid this. The filter should ideally be mounted on or through a bulkhead to completely isolate input from output cables. Alternatively, screened cables should be used on one or both sides of the filter to prevent coupling. Figure 5 shows the effect of not mounting such a filter on a bulkhead or using screened cables. The shaded area shows the loss in high-frequency performance when the filter is not mounted or screened correctly.

ELECTROMAGNETIC INTERFERENCE

Electromagnetic Interference (EMI) occurs in two modes, asymmetric between line and earth, and symmetric between lines. Suppression components fitted to remove one mode of interference may have little or no effect on the other mode, which requires a separate set of components connected differently. When choosing a filter circuit, it is important to know whether only one, or both modes of interference require suppression, so that a filter containing the necessary circuit components can be selected. In simple terms, asymmetric filter performance requires common mode inductors and capacitors from lines to earth, whereas symmetric mode performance requires single-line inductors and capacitors between lines.

Where single-line inductors are used in filters, they will saturate as load current increases, and performance will be lost. The user should always check to see that performance figures quoted relate to full load conditions, as performance at full load current can be a lot worse than no load performance.

In most filtering applications, some asymmetric performance is normally required across the frequency spectrum up to 1GHz. Symmetric performance, where needed, is usually only required below about 10MHz. Some symmetric performance is often provided by board level components.

The insertion loss performance of filters and suppression components is always quoted in a 50Ω system. This has traditionally been considered to represent the characteristic impedance of power lines at radio frequencies. With the widespread use of switching power supplies and power controllers, a much lower source impedance is now more typical. In such cases, a different performance will normally be provided by the capacitor or filter compared to the 50Ω performance shown in the catalogue or datasheet. For most simple filter circuits used in these applications, the actual performance obtained will be worse than expected.

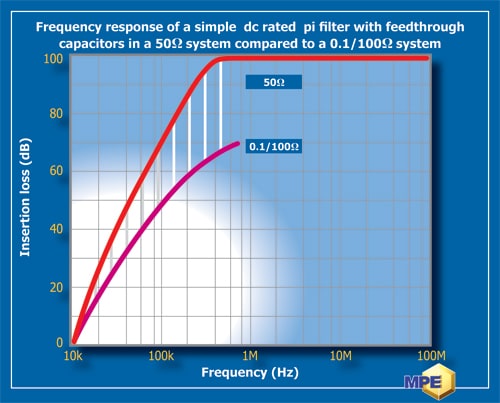
Figure 6A shows an example of the performance of a simple pi filter in a 50Ω system compared with that measured in an impedance of 0.1/100Ω (0.1Ω source and 100Ω load impedance) which might be more typical for a switched mode power supply application. The shaded area shows the significant loss in performance produced in the practical system compared to the quoted 50Ω figures. Although the graph shows a filter with feedthrough capacitors as an example, a filter using two-terminal capacitors would show a similar reduction in performance in the different impedance system. To obtain the required performance in the practical system, it is necessary to tailor the filter circuit to obtain a maximum impedance mismatch between filter and system impedance. This usually means using a filter with an inductive input to face a low impedance noise source.

Another issue of which many users are unaware is that filters can actually produce a gain at certain frequencies due to the mismatch in the impedance between the filter and the source and load impedances. This gain usually occurs at around the cut-off frequency of the filter and is often not apparent or not present when the filter is measured in a 50Ω system. However, in a more practical situation where the source and load impedance are not 50Ω, then the gain can be significant at around 10dB or more.

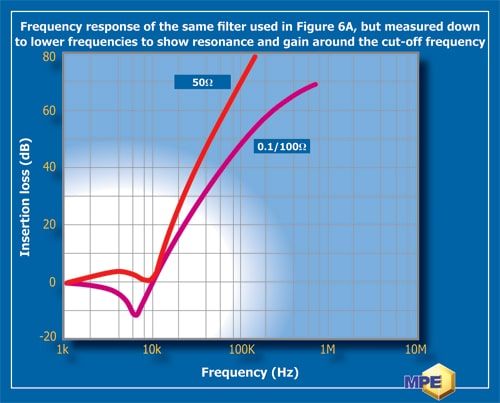
As an example of this, Figure 6B shows a measurement of the same filter as used in Figure 6A but measured down to lower frequencies to show this effect. It can be seen that, in a 50Ω system, there is a resonance around the cut-off frequency of 10kHz but no gain. However, the same filter measured in a 0.1/100Ω system does show a gain of around 12dB at 7kHz.

It must be stated that, although this gain is real, its magnitude and frequency will depend on the actual source and load impedances of the practical circuit, as well as the component values used in the filter circuit. If there is no EMI noise present at the frequency of the gain, then there will be no gain, so the phenomenon should be of no concern. This will usually be the case in practice, as the filter will normally be designed for filtering higher frequency noise. However, there could be applications where there is an issue, and the user should be aware of this possibility.

STANDARD RANGES

There are many types of simple circuit filters available from numerous manufacturers, but most of them could be subject to some or all of the problems described above when used in certain applications. Becoming increasingly important are standard ranges of feedthrough capacitors, and filters incorporating feedthrough capacitors, which are designed to address some or all of the above problem areas. Some of the standard ranges of filters now available not only incorporate feedthrough capacitors but also have filter circuits designed to give the best response with low source impedance. Some manufacturers’ catalogues now also quote performance in both 50Ω and 0.1/100Ω systems, which is more helpful.

Figure 7 shows an example of standard filters incorporating feedthrough capacitors, and which have bulkhead mounting to provide optimum high-frequency performance.

Figure 8 shows an example of a standard filter designed for switched mode power supply applications to offer good performance in a 0.1/100Ω system.

As an alternative, Figure 9 shows an example of a standard range of feedthrough capacitors, which will offer excellent, cost-effective, high-frequency performance where full filter performance is not needed.

SUMMARY

This discussion has identified a few pitfalls, which can cause the anticipated filter or capacitor performance not to be achieved in practice. If a standard catalogue filter is to be used, then the user should ensure that the selected filter design addresses any problem areas above relevant to the application.

This may involve the selection of a slightly more specialized filter. For critical applications, the best approach is to obtain advice on the selection of the best filter circuit to use from a specialist filter company with established practical experience in filtering for EMC. The supplier should be familiar with the type of problems discussed here and therefore be able to provide rapid and accurate advice on the most cost-effective solution for a given application.