Regardless of the accuracy of the modeling tool, each modeling exercise requires some level of validation before simulation results can be trusted.
Bruce Archambeault, Ph.D. and Samuel Connor
IBM
Research Triangle Park, NC
The need to validate simulations and model results has never been more vital. Full-wave and quasi-static simulation tools using many different modeling techniques are in common use for a wide variety of EMI/EMC problems. Given a particular model, software tools will provide an accurate result based on that input or model. Unfortunately, there is no guarantee that the model was created properly, that the essential physics of the problem have been included, or that the results have been interpreted properly. Some extra work must be done to verify that the results are correct for the intended simulation.
There is a sense by some that if a modeling tool has been validated in the past (with measurements or some other technique), then the user can trust all the results from this tool in the future. This assumption is extremely dangerous and should be avoided. Some level of validation should be performed on every group of models to make sure that the geometry is correctly represented, that the source in the model is realistic, and that the results are in accord with the underlying laws of physics. This article will discuss some of the various techniques that can be used to validate full wave simulations.
A number of papers on computational modeling validation have been presented at a wide variety of conferences in the past few years.[1–5]This paper is a summary of the various model validation techniques.
Model Validation Using Measurements
Measurements are the most common way to validate a simulation. In fact, when performed carefully, measurements are an ideal way to validate simulations. However, measurements are not always accurate. Extreme care must be used if simulations are to be validated using measurements.
It is vital that the exact same measurement configuration is used in the simulation. Care must be taken to include measurement limitations in the model. If direct probing methods are used to measure/model printed circuit board effects, then the loading imposed by the test equipment (typically 50 ohms) must be included in the simulation, or the results are not likely to agree. If radiated emissions are to be used for validation, then the ground-reference in the test site, the movement of the antenna from one to four meters above the ground-reference plane (for commercial EMC testing), must be included. Another important consideration is the physical antenna used for the measurement. This antenna will have an antenna factor that varies with frequency and will have significant directionality as well. Typically, modeling tools have ‘perfect’ isotropic antennas, which may measure fields approaching from direct directions much differently than the real-world antenna would.
Another aspect of model validation by measurement is the accuracy of the measurement itself. While most engineers take great comfort in data from measurements, the repeatability of radiated emissions measurements in a commercial EMI/EMC test laboratory is unreliable. The differences between measurements taken at different test laboratories, or even within the same test laboratory on different days, can easily be as high as ±6 dB. The poor measurement accuracy (or repeatability) is due to measurement equipment, antenna factors, site-measurement reflection errors, and cable movement optimization. Often, data from military EMI/EMC laboratories with a plain shielded room test environment are considered to have a much higher measurement uncertainty.
The test environment’s repeatability, accuracy, and measurement uncertainty must be included when evaluating a numerical model’s result against a measurement. The agreement between the modeled data and the measurement data can be no better than the test laboratory’s uncertainty. If measurement data disagree with modeled data, some consideration should be given to the possibility that the measurement was incorrect and the model data correct. Therefore, it is essential to avoid measurement bias and to consider both results as correct equally. When two different techniques provide different results, all that can be logically known is that one of them, or possibly both of them, is wrong.
These caveats do not mean that measurements should never be used for simulation validation. Measurements are especially useful when the test environment is well controlled and repeatable. For example, testing printed circuit boards that have connectors (BNC, SMA, etc.) mounted on the board, and using a network analyzer for the measurements, will provide very repeatable results. As long as the model includes the effects of the source and load impedance that the network analyzer adds to the measurement, the comparison of the modeled and measured results will be valid.
Model Validation Using Multiple Simulation Techniques
Another popular approach to validating simulation results is to model the same problem using two different modeling techniques. If the physics of the problem are correctly modeled with both simulation techniques, then the results should agree. Achieving agreement from more than one simulation technique for the same problem can add confidence to the validity of the results.
There are a variety of full-wave simulation techniques. Each has strengths, and each has weaknesses. Care must be taken to use the appropriate simulation techniques and to make sure they are different enough from one another to make the comparison valid. Comparing a volume-based simulation technique (i.e., FDTD, FEM, TLM) with a surface-based technique (i.e., MoM, PEEC) is preferred because the essential nature of the techniques are so very different. While this approach means that more than one modeling tool is required, the value of having confidence in the simulation results more than justifies the cost of many vendor software tools.
Given the very nature of full-wave simulation tools, structure-based resonances often occur. These resonances have a considerable impact on the validity of the simulation results. Most often, the simulations of real-world problems are subdivided into small portions because of memory and model complexity constraints. These small models will have resonant frequencies that are based on their arbitrary size and will bear no real relationship to the actual full product. Results based on these resonances are often misleading, since the resonance is not due to the effect under study. Rather, it is due to the size of the subdivided model. When evaluating a model’s validity using multiple techniques, care must be taken to make sure that these resonances are not confusing the ‘real’ data. Some techniques, such as FDTD, can simulate infinite planes.* Other techniques allow infinite image planes, etc.*Some FDTD tools allow metal plates to be placed against the absorbing boundary region, resulting in an apparent infinite plane.
Model Validation Using Intermediate Results
Computational modeling provides a tremendous advantage over measurements since physical parameters may be viewed in the computational model although they could never be physically viewed in the real world. Electric fields, magnetic fields, and RF currents on a surface can all be viewed within the computational model, although direct measurement in the laboratory may be difficult.
These parameters are used as an intermediate result within the computational model, and can be very useful to help establish that the model has performed correctly. While the final far-field result may be the goal of the simulation, the intermediate results should be examined to ensure that the model is operating as theory, experience, and intuition require.
One intermediate result that is very useful is the steady-state current at various frequencies. This current can be observed when using integral equation based techniques like MoM and PEEC. The currents should be examined to insure that the amplitude of the current does not vary significantly between adjacent cells. The current must go to zero at the ends of thin wires (like a dipole). Also, the currents must flow in the proper direction. All these considerations require the user to examine the intermediate results for ‘reasonableness’. If the results do not make sense in terms of physics and electromagnetics, then further examination is required.
Another useful intermediate result is the animation of the fields, voltages, or currents in a time domain simulation (FDTD, PEEC, TLM). Observing these quantities versus time can be very helpful, not only for understanding the effects of various parts of the model, but also to assure that the results make sense. Again, an understanding of basic physics and electromagnetics is required. Metal shields should block emissions, currents should flow as expected, and voltages should propagate along PC boards as expected.
Model Validation Using Standard Problems
A number of Standard Validation problems have been proposed over recent years[6–10] to assist engineers who wish to evaluate the various vendor modeling tools against specific problems that are similar to the types of problems that they intend to simulate. A wide variety of problems has been developed, and they are available on the IEEE/EMC Society’s modeling website. Validation problems for printed circuit board problems, antenna-like problems, shielding problems, and benchmark problems, etc. have been specified and can be used to validate both modeling tools and individual models if they are similar to the standard. Results for most of the standard modeling problems have been published, and they can be used directly for comparison with a new model’s results.
Model Validation Using Convergence
There are a number of model parameters that must be decided before the actual simulation can be performed. The size of the grids/cells is often set to lambda/10 to satisfy the assumption that the currents/fields do not vary within each grid/cell. However, this size may not be small enough to capture the currents/fields accurately if the amplitude of the currents/fields varies rapidly on the structure. Changing the size of the grid/cell is a good way to insure that the proper size has been used. If the results change when the grid/cell size is changed, then the correct size was not used. Once the grid/cell size is correct, the final results from the simulation will not change.
With some simulation techniques such as FEM, another convergence check is important. Varying the size of the computational domain assures that there are no spurious responses and that absorbing boundary mesh truncation effects will not interact with the physical model. Again, the final result should not be dependent on the size of the computational domain or the distance between the absorbing boundary mesh truncation and the physical model. If the results are seen to change as these parameters are changed, the model must be modified and re-run until these parameters do not affect the final result of the simulation.

One important consideration when using grid/cell size convergence or computational domain size convergence is the amount of computer random access memory (RAM) required to run the simulation. Often, models are created that require most of the RAM available, and modifying the model for convergence testing may require more RAM than is available. This does not eliminate the need to validate the model. If convergence testing is not possible due to limited RAM, then a different validation approach must be used.
Model Validation Using Known Quantities
Under some circumstances, it is possible to use known quantities to validate a model. For example, the radiation pattern of a half-wave dipole is a well known quantity; and if the model is similar to a half-wave dipole, then a dipole pattern simulation may help increase confidence in the simulation results from the primary model. Another example involves shielding effectiveness simulations. A six-sided completely-enclosed metal enclosure should have no emissions when a source is placed inside the enclosure. However, depending on the implementation, some simulation techniques, such as the Method of Moments (MoM) and most scattered field formulation techniques will show an external field even from a completely enclosed metal box.
Model Validation Using Parameter Variation
Within a model, there are usually a number of parameters that are critical to the model’s results. Size of apertures, number of apertures, and component placement on PCBs can vary the final result of the simulation. In many cases, the effect of changing a parameter can be predicted from experience, even though the actual amount of variation may not be known in advance. In this example, the size of the aperture can be increased, and the shielding effectiveness for the different aperture sizes examined for “reasonableness.” Also, resonant frequencies for the aperture can be seen to vary as the size of the aperture varies, providing another opportunity to check the results from the simulation.
How Well Do the Simulation and Validation Agree?
Once the simulation results have been validated and there are multiple plots to compare, the question becomes just how well do those plots agree. Obviously, if the plots overlap completely, the agreement is very good. However, this is seldom the case, and some comparison methods are needed to quantify the agreement.
Experts will be able to take a quick look at such comparisons and to make informed judgments based on years of experience. However, when engineers/students have less experience, a technique is needed that approximates the judgment calls based on such experience and expertise. Simple subtraction of the two plots is not usually sufficient since resonances may vary slightly in frequency or amplitude causing large differences when subtracting, but actually causing little difference in the simulations.
The Feature Selective Validation (FSV) technique[1, 11, 12, 13] has been developed to mimic the experts and to allow the computer to compare results and to provide a “measure-of-goodness.” The FSV technique uses a combination of the Amplitude Difference Measure (ADM) and the Feature Difference Measure (FDM) to provide the measure of the agreement between two data sets. The ADM gives an indication of how well the overall amplitude of the two data sets agrees, and the FDM provides an indication of how well the rapidly changing features of the two data sets agree. If desired, the ADM and FDM can be combined to give the Global Difference Measure (GDM).
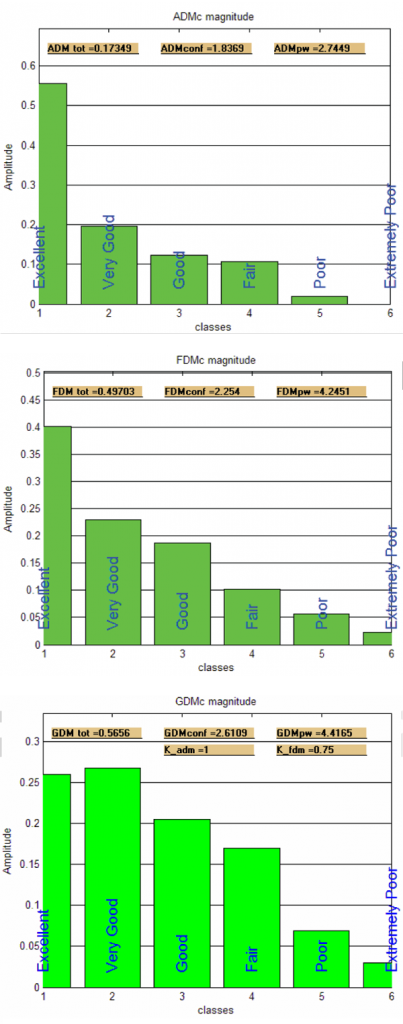
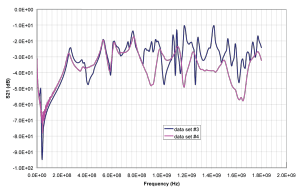
There are a number of different ways the FSV information can be used. The ADM, FDM, and GDM can provide a point-by-point indication of the agreement as well as an overall average result. Instead of an average agreement factor, the FSV can also provide an overall indication of how many data points agree in a histogram fashion. Figure 1 shows an example of two data sets plotted in the same graph. At first glance, most engineers would feel the two data sets agree pretty well. Figures 2a, 2b, and 2c show the confidence histogram for the ADM, FDM and GDM, respectively. The ADM histogram in Figure 2a indicates that approximately 55% of the data points have excellent agreement, and another 20% have very good agreement. Similar judgments are made for the FDM and GDM.
Typically, a threshold of 85% is used to provide an overall GRADE indication of the agreement. In other words, how much of the agreement is required before 85% is reached. Using the ADM in Figure 2a as example, note that for an 85% confidence, the agreement is Excellent-to-Good, resulting in a GRADE of 3. The GRADE indicates how many agreement categories are required before the 85% point is reached.
It is also often useful to see how widely distributed the agreement is between two data points. For example, it is possible to have two data sets that agree only fairly well (GRADE = 4). Still, that numerical designation could indicate an agreement either spread over all the categories from excellent to fair or one in which all the data sets fell into the fair category. Appropriately enough, the SPREAD indicates the distribution—just how far the categories underlying the GRADE are spread apart. The SPREAD starts with the highest category in the histogram (not necessarily the Excellent category) and determines how many categories are required to reach the 85% level. For the ADM in Figure 2a, the SPREAD equals three. Table 1 shows the GRADE and SPREAD for the ADM, FDM, and GDM for this set of data.


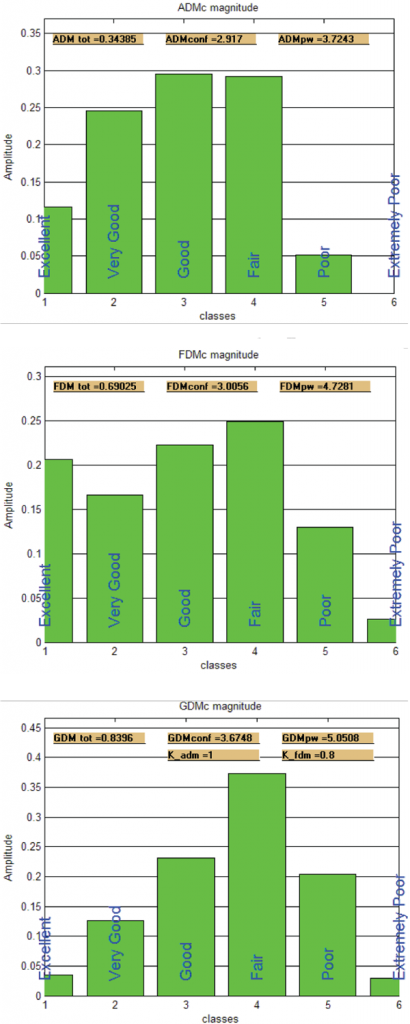
Another example is provided in Figure 3. In this example, the data sets do not agree as well as the example in Figure 1. Figures 4a, 4b, and 4c show the agreement for the ADM, FDM, GDM, respectively, and Table 2 shows the GRADE and SPREAD for this example.
While there is a lot of information that can be derived from the FSV method, at a minimum, the GRADE and SPREAD should be used whenever comparing two sets of data. It is most often used to compare simulation and validation results, but two sets of measured results can also be compared using the FSV (for example, when comparing EMC emissions test results from two different laboratories).
Summary
It is never enough to simply “believe” a model has created the correct answers; engineers must be able to prove it by validating the model. Simulation is usually performed on a computer, and the old adage “Garbage In, Garbage Out (GIGO)” still applies. Engineers should validate their models to ensure the model’s correctness and to gain insight into the basic physics behind the model. Models can be validated by a variety of techniques. The best technique for validating a specific model depends on a number of parameters and should be decided on a case-by-case basis. Measurements can be used to validate modeling results, but extreme care must be used to ensure that the model correctly simulates the measured situation. Omitting feed cables, shielding or ground reflections, or different measurement scan areas can alter the results dramatically. An inexact model result might be indicated when, in fact, the measured and modeled results are obtained for different situations and should not be directly compared.
Multiple simulation techniques applied to the same model is a good way to insure that the correct physics are included in the model and that the appropriate physics are modeled correctly. Care is needed to insure that the modeling techniques are different enough to insure that a meaningful comparison is made. Intermediate results can also be used to help increase the confidence in a model. Using the RF current distribution in a MoM model, or the animation in an FDTD model, can help ensure the final results are correct by determining the accuracy of the intermediate results. These intermediate results have the added benefit of increasing the engineer’s understanding of the underlying causes and effects of the overall problem. There are a number of other possible validation techniques, including using known quantities, model parameter variation, etc. Choosing among the various validation possibilities depends on the exact model and the goal of the simulation.
An indication of how well the simulation and validation results agree is available with the FSV technique. At a minimum the GRADE and SPREAD provide a simple and quick indication of the quality of the agreement between data sets. Ultimately, engineers need to understand the physics of the problem at-hand and must verify that the results obtained are correct. Regardless of the accuracy of the modeling tool for “other” models, each modeling exercise must have some level of validation before the simulation results can be trusted. While every model does not require validation, each group of models or each series of models for similar problems should have some level of validation.
References
- A. Duffy, D. Coleby, A. Martin, M. Woolfson, T. Benson, “Progress in quantifying validation data”, IEEE International Symposium on EMC, Boston, Aug 18–22 2003, pp. 323–28.
- Andrew Drozd, “Progress on the development of standards and recommended practices for CEM computer modeling and code validation”, IEEE International Symposium on EMC, Boston, Aug 18–22, 2003, pp. 313–316
- B. Archambeault, “Concerns and approaches for accurate EMC simulation validation”, IEEE International Symposium on EMC, Boston, Aug 18–22, 2003, pp. 329–334.
- H.-D. Bruns, H.L. Singer, “Validation of MoM Simulation results”, IEEE International Symposium on EMC, Boston, Aug 18–22, 2003, pp. 317–322.
- M.A. Cracraft, X. Ye, C. Wang, S. Chandra, J.L. Drewniak, “Modeling issures for full-wave numerical EMI simulation”, IEEE International Symposium on EMC, Boston, Aug 18–22, 2003, pp. 335–340.
- B. Archambeault, S. Pratapneni, L. Zhang, D.C. Wittwer, “Comparison of various numerical modeling tools against a standard problem concerning heat sink emissions,” IEEE International Symposium on EMC, Montreal, Aug. 13–17, 2001, Vol. II, pp. 1341—1346.
- B. Archambeault, S. Pratapneni, L. Zhang, D.C. Wittwer, J. Chen, “A proposed set of specific standard EMC problems to help engineers evaluate EMC modeling tools,” IEEE International Symposium on EMC, Montreal, Aug. 13–17, 2001, Vol. II, pp. 1335–1340.
- J. Yun, B. Archambeault, T.H. Hubing, “Applying the method of moments and the partial element equivalent circuit modeling techniques to a special challenge problem of a PC board with long wires attached,” IEEE International Symposium on EMC, Montreal, Aug. 13–17, 2001, Vol. II. pp. 1322–1326.
- H. Wang, B. Archambeault, T.H. Hubing, “Challenge problem update: PEEC and MOM analysis of a PC board with long wires attached,” IEEE International Symposium on EMC, Montreal, Aug. 13–17, 2001, Vol II, pp. 811–814.
- B. Archambeault, A. Ruehli, “Introduction to 2001 special challenging EMC modeling problems,” IEEE International Symposium on EMC, Montreal, Aug. 13–17, 2001, Vol. II, pp. 799–804.
- B. Archambeault, A. Roden, O. Ramahi, “Using PEEC and FDTD to solve the challenge delay line problem,” IEEE International Symposium on EMC, Montreal, Aug. 13–17, 2001, Vol II, pp. 827–832, Vol.2.
- General FSV information http://www.eng.dmu.ac.uk/FSVweb/
- Free FSV tool download site http://ing.univaq.it/uaqemc/public_html/FSV_2_0
Bruce Archambeault is an IBM Distinguished Engineer at IBM in Research Triangle Park, NC. He received his B.S.E.E degree from the University of New Hampshire in 1977 and his M.S.E.E degree from Northeastern University in 1981. He received his Ph. D. from the University of New Hampshire in 1997. His doctoral research was in the area of computational electromagnetics applied to real-world EMC problems.
In 1981 he joined Digital Equipment Corporation and through 1994 he had assignments ranging from EMC/TEMPEST product design and testing to developing computational electromagnetic EMC-related software tools. In 1994 he joined SETH Corporation where he continued to develop computational electromagnetic EMC-related software tools and used them as a consulting engineer in a variety of different industries. In 1997 he joined IBM in Raleigh, N.C. where he is the lead EMC engineer, responsible for EMC tool development and use on a variety of products. During his career in the U.S. Air Force, he was responsible for in-house communications security and TEMPEST/EMC related research and development projects.
Dr. Archambeault has authored or co-authored a number of papers in computational electromagnetics, mostly applied to real-world EMC applications. He is currently a member of the Board of Directors for the IEEE EMC Society and a past Board of Directors member for the Applied Computational Electromagnetics Society (ACES). He has served as a past IEEE/EMCS Distinguished Lecturer and Associate Editor for the IEEE Transactions on Electromagnetic Compatibility. He is the author of the book “PCB Design for Real-World EMI Control” and the lead author of the book titled “EMI/EMC Computational Modeling Handbook.”
Samuel Connor received his BSEE from the University of Notre Dame in 1994. He currently works at IBM in Research Triangle Park, NC, where he is a senior engineer responsible for the development of EMC and SI analysis tools/applications.
Mr. Connor has co-authored several papers in computational electromagnetics, mostly applied to high-speed signalling issues in PCB designs.
