Simple Method for Predicting a Cable Shielding Factor, Based on Transfer Impedance

For a shielded cable, an approximate relationship valid from few kHz up to the first cable resonance can be derived from its Transfer Impedance (Zt) allowing to predict the cable shielding factor. This Cable Shielding factor, as a figure of merit, is often preferred by engineers dealing with product specifications and early design. Being not necessarily EMC specialists, they can relate it directly to the overall shielding performance required for a system boxes or cabinets.

This article comes up with very simple, practical formulas that directly express the cable shielding factor Kr, given its Zt and frequency.

INTRODUCTION

Expressing the effectiveness of a cable shield has been a recurrent concern among the EMC community, and, more generally, for the whole electronic industry. This concern comes from a legitimate need to predict, measure, compare and improve the efficiency for a wide variety of shielded cables, such as coaxial cables or shielded pairs and bundles, having themselves various types of screens: braids, foils, spiral, corrugated, woven etc.

However, when it comes to decide what would be a convenient, trustworthy characteristic for a cable shield, several methods are in competition: Shielding Effectiveness (SE,dB), Surface Transfer ( Zt, Ohm/m) or Screen Reduction Factor (Kr, dB).

Although Transfer Impedance Zt is a widely used and dependable parameter, SE or Reduction Factor Kr as a figure of merit are often preferred by engineers dealing with product specifications and overall  design, because they can relate it directly to the whole shielding performance required for the system.  It would be a nonsense to require 60dB of shielding for a system boxes or cabinets if the associated cables and their connecting hardware provide only 30dB, and vice-versa.

a) Shielding Effectiveness, as defined for any shielding barrier is given by:

SE (dB) = 20 log [E ( or H) without shield] / [ E ( or H) with shield]

By illuminating the tested sample with a strong electromagnetic field, this approach is coherent with Shielding Effectiveness definition for a box, a cabinet or any enclosure, with SE being a dimensionless number. Since it would be unpractical to access the remaining E (or H) field inside a cable shield, meaning between the sheath and the core, it is the effect of this incident field that is measured instead, for instance the core-to-shield voltage.

However, there are several drawbacks to this method:

• It requires a full range of expensive instrumentation : generator, power amplifier, antennas, shielded/ anechoic room (or stirred mode reverberating chamber) etc …
• It carries the typical uncertainties of radiated measurements ( mean value for ordinary radiated EMI test uncertainty being 6dB)
• It is very sensitive to the tested cable set-up: height above ground, termination loads and type of excitation in near field conditions. For instance,  a transmit antenna at 1m from the test sample will create near field conditions  for all frequencies below 50MHz. If the antenna is of the dipole family, the near-field will be predominantly Electrical, i.e. a high-impedance field and the SE results will look excellent. If the transmit antenna is a magnetic loop, the field will be a low-impedance H field, and the SE results will be much less impressive.

b) Transfer Impedance (Zt), in contrast to SE, is a purely conducted measurement method, with accurate results, typically within 10% (1dB) uncertainty. But Zt, being in Ohm/meter has a dimension and cannot be directly figured as a shield performance .

c) Shield Reduction Factor, Kr reconciles the two methods, by using the best of Zt – the benefit of a conducted measurement, and of SE : the commodity of a direct  figure in dB.

DEFINITION OF THE SHIELD REDUCTION FACTOR

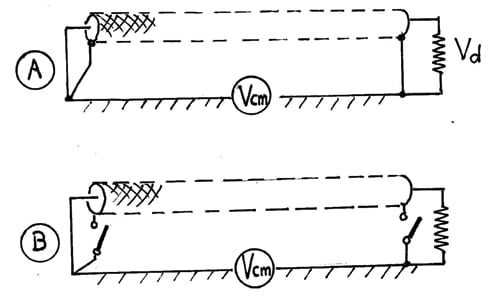
We can define Shield Reduction factor (Kr) as the ratio of the Differential Mode Voltage (Vd) appearing, core-to shield at the receiving end of the cable, to the Common Mode Voltage (Vcm) applied in series into the loop (Figure 1).

Kr (dB) = 20 log (Vd / Vcm)                      (1)

This figure could also be regarded as the Mode Conversion Ratio between the external circuit (the loop) and the internal one ( the core-to-shield line).

Slightly different versions of this definition are sometimes used like:

Kr (dB) = 20 Log (Vd₂ / Vd₁)

Where,

Vd₁ : differential voltage at the receive end when the shield is not there (disconnected)

Vd₂ : differential voltage at the receive end with the shield normally grounded, both ends.

This latter definition would be more rigorous, somewhat reminiscent of the Insertion Loss used in EMC terminology, i.e. it compares what one would get without and with the shield, for a same excitation voltage ( see Fig. 1, B). This eliminates the contribution of the core wire resistance and self-inductance, since they influence identically Vd₁ and Vd₂.

CALCULATED VALUES OF Kr FOR SIMPLE CASES, FOR LENGTH ι < λ/2

Let’s express Vd, using the classical Zt model, assuming that the near end of the cable is shorted (core -to-shield) :

             Vd = Zt x l x I_shield

      where l :  length of the shielded cable

Expressing the shield current,  I_shield

               I_shield = Vcm / Z_loop

We can replace Vd by its value in the expression of Kr:

         

 

Kr = Zt.l / Z_loop

Z_loop itself is a length-dependent term, since it is simply the impedance of the shield-to-ground loop, which for any decent shield is a lesser value than that of the core wire plus the terminal impedances.

               Z_loop (Ω) = ( R_sh + jω. L_ext ) . l

where,

               R_sh =  shield resistance

               L_ext = self-inductance of the shield-to-ground loop

Replacing Z_loop by its expression:

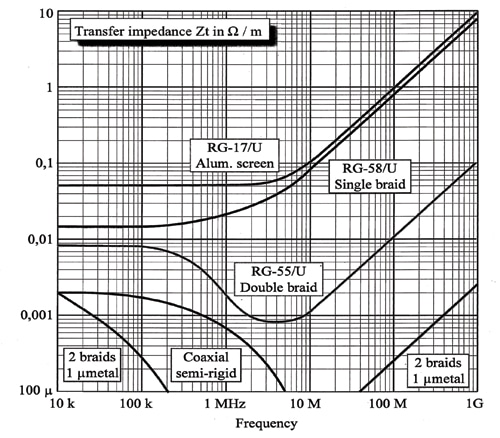
Zt (Figure 2) consists in shield resistance R_shand shield transfer (or leakage) inductance Lt.

Thus, we reach an expression for Kr as a dimensionless number, independent of the cable length:

   (2)

 

This expression is interesting in that it reveals three basic frequency domains:

a) for Very Low Freq., where the term ωLt is negligible, Zt is dominated by R_sh :

Kr = R_sh / ( R_sh + jω. L_ext )

≈ 1 (0dB) below few kHz, since the lower term, loop impedance reduces to Rs_sh

b) at medium frequencies ( typically above 5-10kHz for ordinary braided shield) :

Kr = ( R_sh + jω. Lt ) / ( jω. L_ext )

Reduction Factor improves linearly with frequency

c) at higher frequencies (typically above one MHz), up to first < λ/2 resonance :

      Kr = Lt / L_ext

The Reduction Factor stays constant , independent of length and frequency.

A quick, handy formula can be derived, which is valid for any frequency from 10kHz up to first < λ/2 resonance :

Kr (dB) = – 20 Log [ 1 + (6. FMHz /Zt (Ω/m) ]                                                                         (3)

The value for Zt being that taken at  the frequency of concern.

(*) Several formulas have been proposed in the past for expressing a cable shield effectiveness based on its Zt. An often mentioned quick-rule is : Kr (or SE) dB = 40 – 20 Log ( Zt. l) . Although it are correct  above the ohmic region of Zt, it can give widely optimistic results, like 50dB or 70dB at 50/60Hz where an ordinary shield has no effect at all against Common Mode induced Interference.

CALCULATION OF Kr WHEN LENGTH IS APPROACHING OR EXCEEDING λ/2

When the dimension of the cable reaches a half-wave length, one cannot keep multiplying Zt(Ω/m) by a physical length which is no longer carrying a uniform current. In fact, the “electrically short line” assumption becomes progressively less and less acceptable when cable length “l” exceeds λ/10 .

With the cable being exposed to a uniform electromagnetic field or to an evenly distributed ground shift, a typical case with CM interference, the shield grounded both ends behaves as a dipole exhibiting self-resonance and anti-resonance for every odd and even multiple of λ/2, respectively. Accordingly, current peaks will take place periodically for every odd multiple of λ/2, resulting in a worst-case value of Kr.

*Some tests set-up for measuring Kr are based on end-driving of the cable shield by a 50Ω generator, which introduces also λ/4 resonances. A quick discussion on this artefact is presented in Appendix .

One must also take into account C’, the actual propagation speed in the cable-to-ground transmission line, where C’ is slower than the ideal free-space velocity C. Typically C’ = 0.7 to 0.8 C. Therefore, the actual wavelength in the cable to ground loop is :

λ’ = 0.7 to 0.8 x  λ

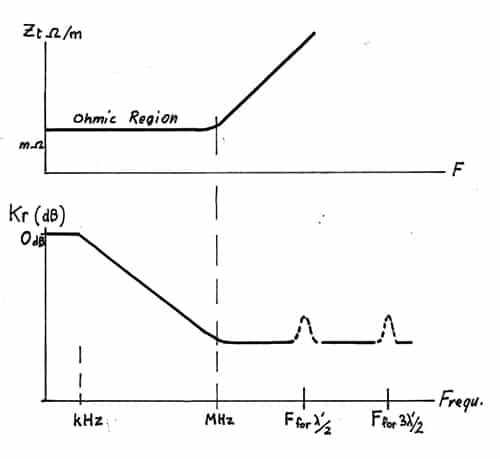
If we align our calculations to the most detrimental conditions, the worst is reached (Figure 3) at the first λ’/2 where the received voltage Vd is maximum (due to a current peak) resulting in a low value for Kr. This is translating correctly the actual situation where, for a uniform field exposure, the victim receiver circuit will see a higher interference.

Beyond this first resonance point, for a constant CM excitation, the termination voltage Vd will run through a succession of peaks ( at odd multiples of λ’/2) and nulls. Yet, the amplitude of the peaks will not exceed that reached at first resonance.

Simply considering that the length of “electrically active” shield segment is limited to  λ’/2, Vd_max can be predicted as follows:

Vd_max = Zt (Ω/m) x 0.5 λ’ x I_shield               (4)

where,

Zt = transfer impedance at frequency of concern corresponding to λ’. At such frequency, Zt is dominated by Lt, the shield transfer inductance

λ’= corrected wavelength for propagation speed C’ ≈  0.7  to 0.8 λ

λ’=  0.75 . 300.10⁶ / F(Hz) = 220.10⁶ / F(Hz) (average value)

(Eq .4) for Vd (max) can be rewritten as:

Vd_max = Lt. ω . 0.5 . ( 220.10⁶ / F ) x I_sh

      =  Lt( H/m). 2π . F. 0.5 . ( 220.10⁶ / F ) x I_sh)

Frequency cancels-out in the equation, so reducing all the variables and using more practical units like Lt in nH/m :

Vd _max ≈ Lt (nH/m) x 0.7 x I_sh                            (5)

We can furthermore express I_shmax for a shield grounded both ends illuminated by a uniform field ( typical EMI susceptibility scenario) :

I_{sh (max)} = I _{loop (max)} = Vcm _max) / Zc

where,

Zc = characteristic impedance of cable-above-ground transmission line

= 150Ω for a height/diam ratio = 4 ( typical of MIL-STD 461 test set-up)

= 300Ω for a height/diam ratio = 50

Thus, Zc can be given an average value of 210Ω ( a + /- 3dB approximation)

Combining Eq. 4 and 5 we get a simple expression for worst case Kr above resonance:

Kr (min) = Vd max / Vcm

= ( 0.7 Lt . Vcm / 210) / Vcm

Kr min (dB) = – 20 Log [ 210 / 0.7 Lt(nH/m) ]

Kr min (dB) = – 20 Log [ 300 / Lt(nH/m) ]  (6)

A FEW PRACTICAL RESULTS FOR Kr, BELOW AND ABOVE FIRST CABLE RESONANCE

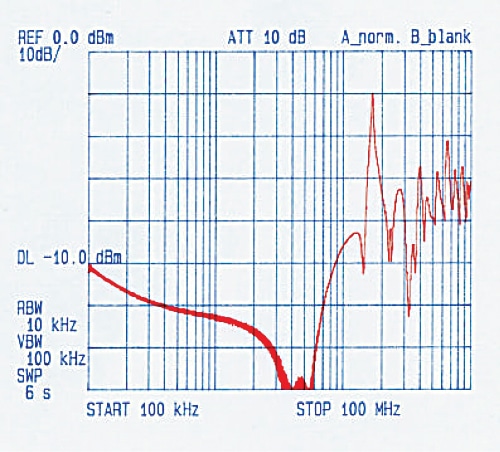
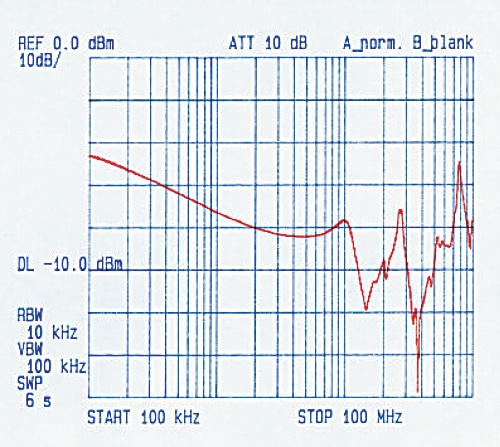
The following figures show some calculations using the formulas of this article, and test results.

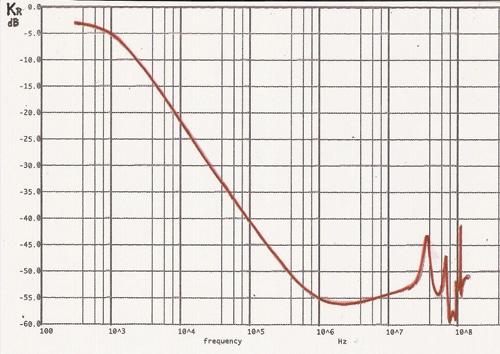
Figure 4 shows calculated results on a 5m long good quality single braid coaxial cable, 1 meter above ground, with perfect 360° contact at connector backshell. On Figure 5, the curve shows the test results of a 5m coaxial cable where the shield has been is intentionally spoiled by a 10cm pigtail. The deterioration of Kr above 8 MHz is spectacular.

APPENDIX

We have seen that when dimension of the cable approaches, or exceeds a half-wave length, the current on the shield follows a sinusoidal distribution with alternating phase reversals every λ/2 segment. This is complicated by the fact that, if the test set-up is based on a 50Ω generator driving one end of the shield, this latter appears as a transmission line shorted at the other end, subject to standing waves.  This mismatch causes nulls and peaks of current at every multiple of λ/4.

For the odd multiples like λ/4, 3 λ/4, 5λ/4 … etc., the null of current correspond to the generator seeing an infinite impedance. While the driving voltage is equal to the open-circuit value,  the current minimum  on the shield is causing a drop in the terminal voltage Vd, therefore the value of Kr artificially jumps to higher values. This effect is visible  on the figures, where Kr appears periodically better, then worse, than its average values. In the present paper, we have preferred to align the calculations on the worst case situation, not the most favorable one.