One of the key elements to making scientific measurements in an EMC lab in today’s modern world is having the engineers understand and control the Measurement Uncertainty (MU) of the instrumentation used for making conducted and radiated emission measurements. The emission levels measured by an accredited lab must have measurement uncertainties below certain levels to be acceptable to its accreditation body. Also, some international standards have begun to quote levels of acceptable measurement uncertainties for electromagnetic emissions. This article outlines a brief history of MU, reviews the MU for equipment used for typical conducted and radiated emission measurements, and give some hints on how a lab can reduce its Measurement Uncertainty for instrumentation used for emission measurements.
General
In this article, Measurement Uncertainty will refer to the Instrumentation’s Measurement Uncertainty. At first glance, MU is a complex subject, however, with a little study it becomes more understandable and more easily understood. Most practicing engineers are familiar with tolerances and error and similar terms. In general, the concept of MU is not as well known. One of the reasons for this is that the theory and practice of measurement uncertainty has only been around about 20 years.
BRIEF HISTORY OF MEASUREMENT UNCERTAINTY
The ISO/IEC Guide 98-3 is the “father” of all Measurement Uncertainty documents. It is commonly just called the “GUM.” It was first released in 1993 and, then, corrected and reprinted in 1995. It changed the world of measurements and the associated errors of measurement instrumentation.
The world’s highest authority in metrology, CIPM (Comite International des Poids et Mesures) realized that there was a need to convene the world’s experts on Measurement Uncertainty in order to arrive at a consensus position on the subject. In 1977, the CIPM requested the BIPM (Bureau International des Poids et Mesures) to communicate with the national metrology laboratories around the world and assess the situation.
By early 1979, responses had been received from 21 laboratories and the great majority of the labs thought that something needed to be done. Specifically, the labs thought that “it was important to arrive at an internationally accepted procedure for expressing measurement uncertainty and for combining individual uncertainty components into a single total uncertainty.”
A working group was formed, developed a process, and released Recommendation INC-1 on Expression of Experimental Uncertainties in 1980. This Recommendation was approved by the CIPM in 1981 and reaffirmed by the same body in 1986.
The ISO (International Organization for Standardization) was given the responsibility of developing a detailed Guide based on the 1980 Recommendation. The responsibility was assigned to ISO Technical Advisory Group on Metrology (TAG 4) which promptly established Working Group 3 comprised of experts nominated by BIPM, IEC (International Electrotechnical Commission), ISO, and OIML (International Organization of Metrology). This TAG labored throughout the 1980s and into the early 1990s to produce the “Guide to the Expression of Uncertainty in Measurement” in 1993. This guide was corrected and reprinted in 1995 and then eventually published as ISO/IEC Guide 98-3 in 2008.
Because of its historical significance, Recommendation INC-1 (1980) is reproduced below for your convenience.
Recommendation INC-1 (1980) – Expression of Experimental Uncertainties
1. The uncertainty in the result of a measurement generally consists of several components which may be grouped into two categories according to the way in which their numerical value is estimated:
A. those which are evaluated by statistical methods
B. those which are evaluated by other means
There is not always a simple correspondence between the classification into categories A or B and the previously used classification into “random” and “systematic” uncertainties. The term “systematic uncertainty” can be misleading and should be avoided.
Any detailed report of the uncertainty should consist of a complete list of the components, specifying for each the method used to obtain its numerical value.
2. The components in category A are characterized by the estimated variances s2i (or the estimated “standard deviations” si ) and the number of degrees of freedom vi. Where appropriate, the covariances should be given.
3. The components in category B should be characterized by quantities u2j, which may be considered as approximations to the corresponding variances, the existence of which is assumed. The quantities u2j may be treated like variances and the quantities uj like standard deviations. Where appropriate, the covariances should be treated in a similar way.
4. The combined uncertainty should be characterized by the numerical value obtained by applying the usual method for the combination of variances. The combined uncertainty and its components should be expressed in the form of “standard deviations.”
5. If, for particular applications, it is necessary to multiply the combined uncertainty by a factor to obtain an overall uncertainty, the multiplying factor used must always be stated.
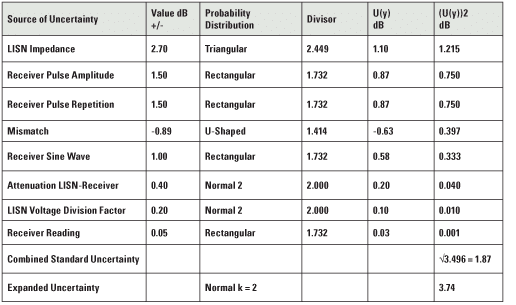
Table 1. 150 kHz to 30 MHz with a 50 ohm/50 microhenry Line Impedance Stabilization Network (LISN).
REFERENCES FOR MEASUREMENT UNCERTAINTY
ISO/IEC Guide 98-3 – Uncertainty of Measurement – Part 3: Guide to the Expression of Uncertainty in Measurement (GUM: 1995).
IEC CISPR 16-4-2: Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods – Part 4-2: Uncertainties, Statistics and Limit Modeling – Uncertainty in EMC Measurements -First Edition – 2003-11.
United Kingdom Accreditation Service – LAB34 – The Expression of Uncertainty in EMC Testing – Edition 1 – August 2002.
Two Examples of Measurement Uncertainty – Conducted Emissions and Radiated Emissions
The following paragraphs go into detail on the MU for instrumentation for conducted and radiated emissions. The presentation of the table is different from what is seen in the usual MU references; namely CISPR 16-4-2 and LAB34.
First of all, we have listed our Sources of Uncertainty in the two accompanying tables in order of the largest contributor to the smallest contributor. This allows us to see which Source is contributing the most to the Measurement Uncertainty.
Secondly, we are going to assume the sensitivity coefficient is one for all our contributing factors thus eliminating one column in our table of standard uncertainties (the sensitivity coefficient is effectively a conversion factor from one unit to another). This is logical in the EMC Engineering world since almost every contributing factor is quoted in “dBs.”
Our table then becomes easier to understand with the Value of the Sources of Uncertainty (second column) being divided by its accompanying Probability Distribution Function Divisor (fourth column) to arrive at the standard uncertainty for that uncertainty component [U(y)] in the fifth column. The sixth column is arrived at by simply squaring the “result in the fifth column.” Summing all the factors in the sixth column and taking the square root of the total, we arrive at the Combined Standard Uncertainty. The Expanded Uncertainty is achieved by multiplying the Combined Standard Uncertainty by two for a coverage of 95%. The Expanded Uncertainty is the engineer’s “padding factor” to make sure he has the answer covered in the range of values quoted.
By using the Expanded Uncertainty, we arrive at a 95% probability that the true answer lies within a band of values bracketed by the measured value plus or minus the Expanded Uncertainty.
CONDUCTED EMISSIONS
The above table assumes typical values from LAB34 and CISPR 16-4-2 and is ordered from the largest contributor to the smallest contributor. In order to reduce the Combined Standard Uncertainty, the lab should start with the largest contributors and try to reduce their values.
In the case of the conducted emissions, the largest contributor is the LISN Impedance.
A check of the calibration certificate of one of the well-known calibration labs in the country indicates a maximum measurement uncertainty of plus or minus 1.2 ohms for a LISN Calibration. This maximum uncertainty was arrived at by the calibration lab by a Type A evaluation using at least 10 data sets. The 1.2 ohms translates into a value in dBs equivalent to +/- 1.6 dB. If we substitute this 1.6 dB value into the table for the present 2.7 dB, we lower our combined standard uncertainty to 1.71 dB which lowers our Expanded Uncertainty to 3.42 dB or a reduction of 0.32 dB. One of the reasons that the LISN factor reduction does not make a big difference is that it is divided by the square root of 6 (2.449) for a triangular distribution.
We would next have to look at the biggest contributors to the Measurement Uncertainty after the LISN Impedance. They would be the Receiver Pulse Amplitude and the Receiver Pulse Repetition. One way to reduce these two contributions from the Receiver is to have it calibrated a number of times (it could be over a period of years). Then, you can divide the “mean value of n measurements” by the square root of “n” to arrive at the standard deviation of the mean. If we could lower the two receiver 1.5 dB values to 1.0 dB,(in tandem with lowering the LISN contribution), we would arrive at a combined standard uncertainty of 1.45 dB or an Expanded Uncertainty of 2.90 dB.
All the other sources of uncertainty in the conducted emission table are 1.0 dB or less, and, it will be difficult to lower those to make a significant change in the total MU for conducted emissions.
So, we can conclude that it would be very difficult to get the Expanded Uncertainty of conducted emissions below 3 dB.
Table 2. 30 MHz to 300 MHz with a biconical antenna in the vertical polarization – 3 & 10 meters.
RADIATED EMISSIONS
30 MHz to 300 MHz with a biconical antenna in the vertical polarization – 3 & 10 meters
Again, the above table assumes typical values from LAB34 and CISPR 16-4-2 and is ordered from the largest contributor to the smallest contributor. In order to reduce the measurement uncertainty for radiated emissions, an EMC lab should start with the largest contributors and try to reduce their values.
The table also assumes a horizontally-polarized biconical antenna having a uniform pattern in the vertical plane so that the antenna factor height deviation and the antenna factor directivity difference contributions are zero. (Note – a Complex antenna would have non-zero components for both of those factors).
The Site Imperfections is the largest contributor to the Radiated Emission Measurement Uncertainty. In order to reduce that, labs can use antennas with smaller antenna factors, receivers with smaller measurement uncertainties, and semi-anechoic chambers with improved anechoic material. It would then be reasonable for the lab to lower that contribution to plus or minus 3 dB. Substituting that value into the equation, gives us a Combined Standard Uncertainty of 2.26 dB and an Expanded Uncertainty of 4.52 dB or a reduction of 0.48 dB from the original 5.00 dB. Again, one of the reasons for the relatively small reduction in the expanded uncertainty is the large divisor value for site uncertainty, that is, the square root of 6 (2.449) for a triangular probability distribution.
The Mismatch factor can be reduced by increasing the attenuation of the well-matched two port network preceding the receiver, however, the penalty of that maneuver is a reduction in measurement sensitivity. Let’s assume we can add some attenuation to the front-end of the receiver and lower the Mismatch contribution to -0.65. Substituting this value in combination with the Site Imperfection reduction, allows us to lower the Expanded Uncertainty to 4.3 dB or a total reduction from the original 5.00 dB of 0.7 dB.
If we then look at the next two biggest contributions, we have, again, the Receiver Pulse Amplitude and the Receiver Pulse Repetition. If we again, using the same technique as for conducted emissions, lower the two receiver 1.5 dB values to 1.0 dB,(in tandem with lowering the Site Imperfections and the Mismatch contributions), we would arrive at a combined standard uncertainty of 1.83 dB or an Expanded Uncertainty of 3.66 dB. This would be a reduction of 1.34 dB from the original value.
The Remaining Factors are all 1.0 dB or less and they would be difficult to lower in sufficient amplitude to make a significant difference to the Expanded Measurement Uncertainty for radiated emissions.
Thus, we conclude that the minimum value for Expanded Uncertainty for radiated emissions, with present-day equipment, is around 3.5 dB.
SUMMARY
Measurement Uncertainty of the instrumentation used for emission testing in an EMC Lab is an important part of the lab’s overall technical capability. We know that Measurement Uncertainty is a relatively new concept and has only been around the EMC Labs of the world for about 20 years.
We see from the above two specific examples that it is difficult to lower the Expanded Uncertainty values of a typical EMC Lab for both conducted emissions and radiated emissions.
We saw that reducing the two largest values in the table of standard uncertainties for conducted emissions only lowered the Expanded Uncertainty by about 0.74 dB so that the Expanded Uncertainty for conducted emissions was approximately 3.0 dB.
We also observed that lowering the top four contributors to the Combined Standard Uncertainty value for radiated emissions, only lowered the Expanded Uncertainty value from 5 dB to around 3.5 dB.
We concluded that even when a lab is logically concentrating on lowering its Equipment Measurement Uncertainty by reducing the largest contributors to the Combined Standard Uncertainty for emission testing, it is difficult to significantly lower the overall Expanded Uncertainty of the instrumentation of the EMC lab for conducted and radiated emissions.
Daniel Hoolihan is a past president of the IEEE EMC Society. He has been a member of the Board of Directors since 1987 and has held numerous leadership positions in the society. Hoolihan is also active on the ANSI Accredited Standards Committee on EMC, C63 as Vice Chairman. He was co-founder of Amador Corporation (1984-1995). He can be reached at DanHoolihanEMC@aol.com.