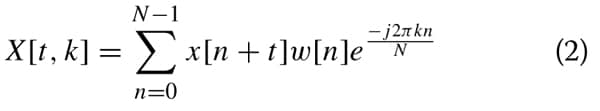More information and reduced measurement time can significantly improve the quality of emissions testing.
Stephan Braun and Peter Russer
Institute for High Frequency Engineering, Munich University of Technology, Munich, Germany
For some time, measurements of electromagnetic interference have been carried out by super-heterodyne receivers operating in the frequency domain. E.L. Bronaugh mentions in his article “An Advanced Electromagnetic Interference Meter for the Twenty-First Century” that, in the future, the conventional technology of super-heterodyne EMI receivers will be replaced by digital emission measurement systems.1
For the past six years, we have carried out research on emission measurements in the time domain.2 The rapid development of digital technology and the increased speed of the analog-to-digital converters make it possible to digitize and store data at speeds of several giga-samples/second (GS/s). Articles in several technical publications have indicated that a digital storage oscilloscope can effectively digitize and store emission signals. For signal processing (i.e., calculation of the spectrum by fast Fourier transform (FFT) and simulation of the detector modes) a conventional PC may be used.3, 4
Typically, digital storage oscilloscopes use an 8-bit analog-to-digital converter with a limited effective number of bits. Clearly, the dynamic range of such a system is not sufficient for handling such transient input signals.5 The dynamic range is decreased by the spurious response of the analog-to-digital converters and by other spurious signals that are added by digital storage oscilloscopes.4 The acquisition memory of the oscilloscope is limited, and it is impossible to store the signal for the entire dwell time. Consequently, the digitization process is impeded by a number of interruptions. Methods for characterizing the signal using a statistical model and performing a quasi-peak detection have been discussed in Braun et al.6 The international EMC Standard CISPR 16-1-1 requires a spurious-free dynamic range for broadband transient signals of 36 dB and a spurious-free dynamic range of 40 dB for stationary signals.7 CISPR also requires a continuous evaluation of the signal without any gaps.
REAL-TIME TIME-DOMAIN EMI MEASUREMENT SYSTEM
In the time-domain EMI (TDEMI) measurement system, the input signal is digitized by an analog-to-digital converter (ADC) unit. Spectral estimation is performed by FFT. The block diagram of a multi-resolution TDEMI measurement system is shown in Figure 1. The EMI signal is received via an ultra broadband antenna.8 A multi-resolution analog-to-digital converter (ADC) system carries out a floating point analog-to-digital conversion.9 The measured and digitized EMI signal is processed via digital signal processing, and the amplitude spectrum is then displayed. The operation of a real-time operating multi-resolution time-domain EMI measurement system has been described in Braun et al.10 Using a frequency scan in the range 30 MHz to 1 GHz, with a step of 50 kHz, a reduction of the measurement time by a factor of 2000 has been achieved.
Fast Fourier Transform
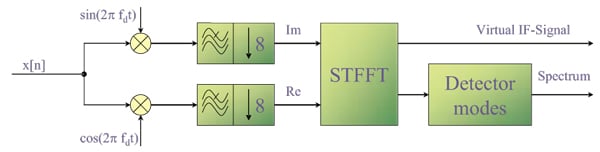
Digital spectral estimation is performed via the discrete Fourier transform (DFT). Algorithms for DFT computations that exploit the symmetry and repetition properties of the DFT are defined as FFT. The DFT formulation considers periodic repetition of the time-domain signal and is given as follows:
Short-Time Fast Fourier Transform
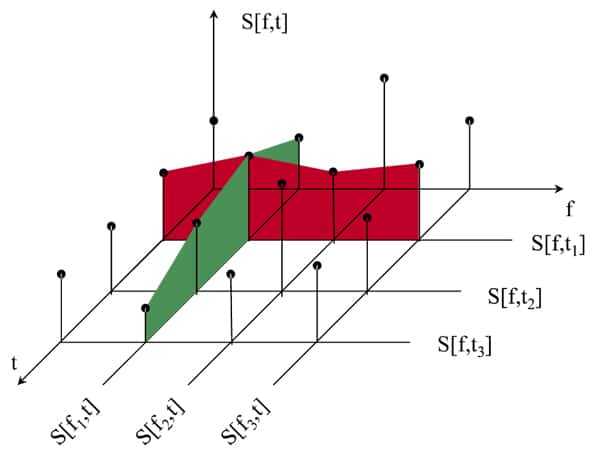
A spectrogram is calculated using a short-time fast Fourier transform (STFFT). This spectrogram shows a discretization in frequency and time. The resolution in frequency is described by the bin-width ∆ƒ. The resolution in time is described by a time step TsBB. The inverse of the time-step is called baseband sampling frequency or fsbb. The STFFT is calculated as follows:
where w[n] is a Gaussian window function that models the IF-filter of an EMI receiver.11 The relation of the baseband sampling frequency fsbb and the bin-width ∆ƒ describes the overlap factor of the STFFT. The discretization in the time domain must be high enough to fulfill the Nyquist criterion.
Hardware Implementation

In Figure 2, a picture of the analog-to-digital converter system is shown. Three 10-bit, 2.2-GS/s ADCs process three amplitude resolutions in this multi-resolution system. The reconstruction and error correction, as well as the real-time spectral calculation, are performed on FPGAs.10 The current measurement system can perform the emission measurement in the peak, average, RMS (root mean square), and quasi-peak detector mode.
Measurement Procedure
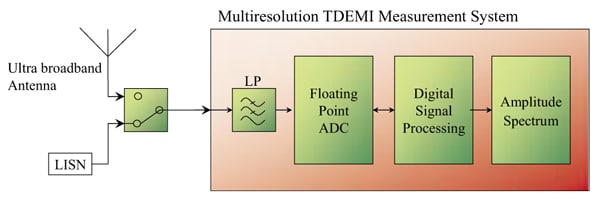
EMI Receivers. Measurements of emissions are traditionally performed by measurement systems operating in the frequency domain. During the dwell time, the input signal is observed at a single frequency and is measured with a detector (e.g., the quasipeak detector). Throughout the complete dwell time, the signal is processed continually via the analog and digital stages of an EMI receiver. The complete characterization of a device-under-test (DUT) may take several hours because of the long dwell times imposed by the time constraints of the detection mode or by the intermittent disturbance of the DUT. The stepped measurement procedure is shown in Figure 3.
Single-Shot Measurement in Time Domain. Time-domain EMI measurement systems capture for the record time trec the EMI Signal and store it. The signal is processed by the fast Fourier transform. The IF filter is modeled with a Gaussian windows function. Using the short-time fast Fourier transform, the recorded signal can be processed, and a spectrogram can be generated. Using a digital simulation of the detector modes, the spectra under the peak, average, quasi-peak, and RMS detector modes are calculated. However, the record time trec is limited by the available high-speed memory. Today, several hundred µs can be recorded, but the detector modes, such as the quasi-peak detector, require a dwell time of about 1.5 s. The procedure for such a measurement system is shown in Figure 3. With this type of system, the measurement time can be reduced by up to five orders of magnitude. Clearly, the drawback to such a system is the limited depth of the high speed memory. A continuous disturbance analysis as mandated by CISPR 14 simply cannot be achieved with this system.
Real-Time, Time-Domain EMI Measurement System. To solve this problem, a real-time, time-domain EMI measurement system has been implemented.12 The measurement system performs the signal processing in real time without the digitized signal. The digitized signal is processed continuously. With currently available digital hardware, it is not feasible to calculate the STFFT in real time over a frequency range of DC to 1 GHz. Consequently, the frequency range to 1 GHz is subdivided into eight bands that are processed sequentially. The measurement procedure is shown in Figure 3. All eight sub-bands are processed sequentially. Each sub-band is processed in real time by the real-time, time-domain EMI Measurement System.
Digital Signal Processing
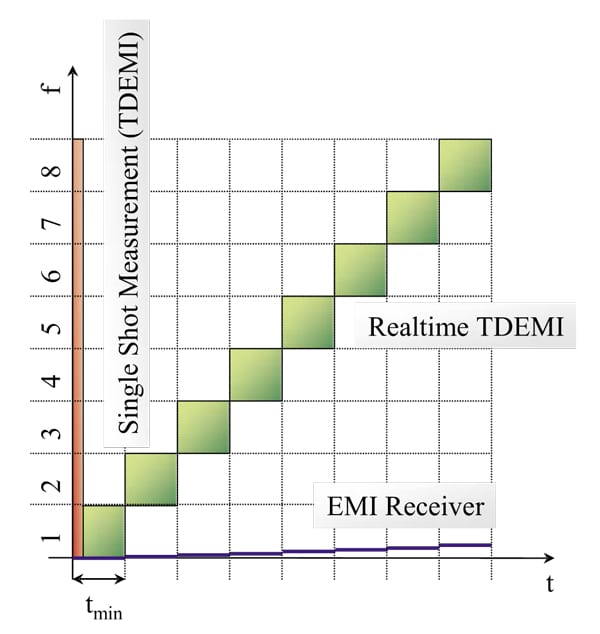
The digitized input signal of 2.2 GS/s is processed using a digital down-conversion unit that consists of a digital I-Q down-converter followed by a polyphase decimation filter. The block diagram is shown in Figure 4. The down-sampled signal is processed via a short-time fast Fourier transform (STFFT) unit. The calculation of the STFFT is described by Krug et al.2 The signal is multiplied with a Gaussian window function that models the IF-Filter of an EMI Receiver. After the calculation of each individual FFT, the window is moved by the time-step Tsbb. With an overlapping factor of 75 percent, a baseband sampling frequency of 250 kHz is achieved. With this technique, a spectrogram is calculated that shows a discretization in both time and frequency. An example of such a spectrogram is shown in Figure 5. At a single frequency ƒithe signal sbb(t) = S[ƒi; t] can be extracted. This signal corresponds to the demodulated IF Signal of an EMI Receiver. At each discrete frequency, the signal is evaluated by a digital detector (e.g., peak, quasi-peak, average, and RMS detector modes). To fulfill all the provisions of CISPR 16-1-1, the IF signal must be provided by an analog output. The signal sbb(t) is digitally mixed to a selected frequency, and a virtual IF signal is generated. The virtual IF signal is converted to an analog IF signal by a digital-to-analog converter followed by a bandpass filter.
EMC STANDARDS
The CISPR 16-1-1 and ANSI C63.2-199613 standards require a continuous observation of the input signal when a single frequency is selected. This requirement can be achieved by mixing the signal into an intermediate frequency (IF), analog IF filter, or an analog detector. In Boss14, it has been shown that the quasi-peak detector can also be implemented using a digital signal processing unit. Today’s EMI receiver implement even the IF filter as a digital filter. STFFT is a signal processing method that performs a continuous signal processing. In Oppenheimer15, it has also been shown that the STFFT corresponds to a bank of N Filters where N is the number of frequency bins. The requirements of CISPR 16-1-1, as well those of ANSI 63.4, can be met by measurement systems that use the STFFT. Such systems must fulfill all the requirements listed in the standards. A minimum spurious-free dynamic range of 40 dB for sinusoidal must be achieved (CISPR 16-1-1). For single broadband pulses during a notch filter test, a minimum spurious-free dynamic range of 36 dB must be achieved.7 An IF-overload factor, which corresponds here to the dynamic range after the FFT calculation, must be at least 43.5 dB. The use of an analog IF signal allows for the connections of a disturbance analyzer for measurements per CISPR 14. A joint task force has been formed to adapt the standards CISPR 16-2 and CISPR 16-3 to time domain EMI measurement systems that are based on the fast Fourier transform. Also, some minor changes to CISPR 16-1-1 have been discussed.
EMISSION MEASUREMENTS

An emission measurement of a laptop was performed. The measurement was carried out in the quasi-peak detector mode. The emission measurement was performed using the multi-resolution time-domain EMI measurement system. The result is shown in Figure 6. An excellent agreement between the measurement performed with the EMI receiver ESCS 30 and the time-domain EMI measurement system was achieved.
LONG-TERM STABILITY ANALYSIS
A long-term stability analysis is an evaluation method of the time-domain emi measurement system that combines the spectrogram view method with CISPR compliant spectral calculation and weighting with a detector mode. An application of this method is the investigation of the device-under-test emissions for a longer period of several seconds. Other applications include the real-time investigation of EMC measurements and the effects that the software of a device-under-test have on the emission.
During the dwell time, the continuous real-time spectral estimation is performed. One of the eight sub-bands can be processed in real-time. A spectrum with a modelled IF bandwidth of 120 kHz in the Peak and Average detector modes is obtained. After the evaluation by the Peak or Average detector during the dwell time, the detector is cleared and a new measurement is initialized. In this way slow changing emissions can be investigated. The peak detector mode is used to investigate EMI signals like bursts and pulse trains that show a strong instationary behavior . The average detector is used to investigate slow changing narrowband emissions with a lower amplitude level.
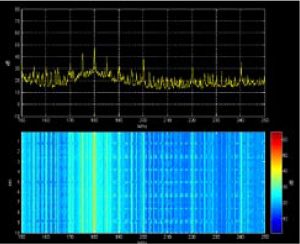

As an example of such a measurement, the emission of a laptop has been investigated. During the measurement, a hard disc defragmentation tool was running. The result of the measurement is shown in Figure 7. It can be seen clearly that a single emission that may be the result of the hard disc access occurs about every second.
The emission measurement was repeated in the average detector mode and with a different polarization. The result is shown in Figure 8.
During the measurement, it is shown that most of the narrowband emissions also exhibit stationary behavior over a longer time.
CONCLUSION
We have presented a time-domain EMI measurement system. The emission measurement system uses a floating point ADC to improve the dynamic range and real-time signal processing to perform an evaluation of the EMI signal without any gaps. Because the requirements of international EMC standards can be met using such a measurement system, conventional EMI receivers can be replaced by using time domain measurement systems up to 1 GHz. Further analysis methods, as well as the reduction of the measurement time by more than three orders of magnitude, have been demonstrated. The additional information obtained by the time-domain EMI measurement system and the reduced measurement time can significantly improve the quality of emissions testing.
REFERENCES
[1] E. L. Bronaugh, “An Advanced Electromagnetic Interference Meter for the Twenty-First Century,” in 8th International Zurich Symposium On Electromagnetic Compatibility, Zurich, Switzerland, 1989, pp. 215–219, no. 42H5, 1989.
[2] F. Krug and P. Russer, “Ultra-fast Broadband EMI Measurement in Time-Domain Using Classical Spectral Estimation,” in 2002 IEEE MTTS International Microwave Symposium Digest, June 2–6, Seattle, USA, pp. 2237–2240, 2002.
[3] F. Krug, T. Hermann, and P. Russer, “Signal Processing Strategies with the TDEMI Measurement System,” in 2003 IEEE Instrumentation and Measurement Technology Conference Proceeding, May 20–22, Vail, USA, pp. 832–837, 2003.
4. F. Krug and P. Russer, “Statistical Evaluations of Time-Domain EMI Measurements,” in 2003 IEEE International Symposium On Electromagnetic Compatibility Digest, May 11–16, Istanbul, Turkey, pp. –, no. TH–P– R2.2, 2003.
5. S. Braun and P. Russer, “The Dynamic Range of a Time-Domain emi Measurement System Using Several Parallel Analog to Digital Converters,” in 16th International Zurich Symposium on Electromagnetic Compatibility, February 13–18, Zürich, Switzerland, 2005.
6. S. Braun, M. Aidam, and P. Russer, “Development of a Multiresolution Time-Domain EMI Measurement System that Fulls CISPR 16-1,” in 2005 IEEE International Symposium On Electromagnetic Compatibility, Chicago, USA, pp. 388–393, 2005.
7. CISPR16-1-1, Specification for radio disturbance and immunity measuring apparatus and methods Part 1-1: Radio disturbance and immunity measuring apparatus – Measuring apparatus. International Electrotechnical Commission, 2003.
8. Rohde & Schwarz, Ultra Broadband Antenna HL562 ULTRALOG. Data sheet, 2001.
9. S. Braun and P. Russer, “A Low-Noise Multi-resolution High-Dynamic Ultra-Broad-Band Time-Domain EMI Measurement System,” IEEE Transactions on Microwave Theory and Techniques, vol. 53, pp. 3354–3363, Nov 2005.
10. S. Braun, M. Al-Qedra, and P. Russer, “A Novel Realtime Time-Domain EMI Measurement System Based on Field Programmable Gate Arrays,” in 17th International Zurich Symposium on Electromagnetic Compatibility, Digest, (Singapore), pp. 501–504, Feb. 2006.
11. S. Braun, F. Krug, and P. Russer, “A Novel Automatic Digital Quasi-peak Detector for a Time-Domain Measurement System,” in 2004 IEEE International Symposium On Electromagnetic Compatibility Digest, August 9–14, Santa Clara, USA, vol. 3, pp. 919–924, Aug. 2004.
12. S. Braun and P. Russer, “A Novel Multi-Source Model to Predict the Radiated Emissions with a Time-Domain EMI Measurement System,” in 17th International Zurich Symposium on Electromagnetic Compatibility, Topical Meetings, (Singapore), pp. 221–224, Feb. 2006.
13. ANSI C63.2-1996, American National Standard for Electromagnetic Noise and Field Strength Instrumentation, 10 Hz to 40 GHz- Specifications. The Institute of Electrical and Electronics Engineers (IEEE), Inc., 1996.
14. H.F. Boss, “Development of a Novel Digital Quasi-peak Detector for EMI Measurements,” in 14th International Zurich Symposium On Electromagnetic Compatibility, Zurich, Switzerland, 20.–22.2.2001, pp. –, no. 68K5, 2001.
15. A.V. Oppenheim and R.W. Schafer, Discrete–Time Signal Processing. ISBN 0-13-214107-8, Prentice-Hall, 1999.
ABOUT THE AUTHORS
Stephan Braun was born in Überlingen/Germany 1978. He studied electrical engineering at the Munich University of Technology (TUM) were he received his Dipl.-Ing. Degree in 2003. Since 2003 he is working towards his Dr.-Ing. Degree at the Institute of High-frequency Engineering at the same University.
His research interests are high-frequency circuit design, digital signal processing and digital circuits. His research is focused on the investigation of Electromagnetic Compatibility in time-domain. Stephan Braun has been author and co-author of more than 20 publications and several patents. In 2006. he won a best student paper prize at the 17th International Zurich Symposium in Singapore. Stephan Braun is a Student Member of IEEE. Stephan Braun is a Member of the German Verband der Elektrotechnik und Informationstechnik (VDE) and VDE/VDI-Gesellschaft Mikroelektronik, Mikro- und Feinwerktechnik (GMM).
Peter Russer received his Dipl.-Ing. degree in 1967 and his Dr. techn. degree in 1971, both in electrical engineering and both from the Vienna University of Technology, Austria, where he was Assistant Professor from 1968 to 1971 and worked on the AC Josephson Effect. In 1971 he joined the Research Institute of AEG-Telefunken in Ulm, Germany, where he worked on fiber optic communication, broadband solid-state electronic circuits, statistical noise analysis of microwave circuits, laser modulation and ber optic gyroscopes. In 1979 he was co-recipient of the NTG Award for the publication “Electronic Circuits for High Bit Rate Digital Fiber Optic Communication Systems” Since 1981 he has been professor and head of the Institute for High Frequency Engineering at the Technische Universität München, Germany. In 1990 he has been Visiting Professor at the University of Ottawa, and in 1993 he has been Visiting Professor at the University of Victoria. From October 1992 through to March 1995 he was director of the Ferdinand-Braun-Institut f¸r Hˆchstfrequenztechnik, Berlin/Germany.
In 1994, he was elected to the grade of Fellow of the IEEE for fundamental contributions to noise analysis and low-noise optimization of linear electronic circuits with general topology. From 1997 to 1999 he has been Dean of the Department of Electrical Engineering and Information Technology of the Technische Universit‰t M¸nchen. From 1997 to 2004 he has been member of the Board of Directors of the European Microwave Association and in 1999 he has been the General Chairman of the European Microwave Week held in Munich.
Russer has published more than 590 scientific papers in refereed journals and conference proceedings. He has developed a variety of courses in RF techniques, microwaves, quantum electronics and optical communications.
Russer is the program director of the international graduate program “Master of Science in Microwave Engineering” at the TUM. Over the years he has graduated more than 500 students of which more than 50 received their PhD degree. So far eight of his former students have become professors. He has served as a member of the technical programme committees and steering committees of various international conferences (IEEE MTT-S, European microwave Conference and as the member of the editorial board of several international journals (Electromagnetics, International Journal of Numerical Modeling). From 1999 to 2002 he has been Co-Chair and from 2002 to 2005 he has been Chair of the U.R.S.I. Commission D. In 2006 he received the Distinguished Educator Award of the IEEE MTT Society. His current research interests are electromagnetic fields, numerical electromagnetics, metamaterials, integrated microwave and millimeter-wave circuits, statistical noise analysis of microwave circuits, time-domain measurement methods in EMC, and methods for computer-aided design of microwave circuits. Peter Russer is Fellow of the IEEE, member of the German Informationstechnische Gesellschaft (ITG) and the German as well as the Austrian Physical Societies.