Michel Mardiguian, EMC Consultant, Saint-Rémy-lès-Chevreuse, France
The concept of Shield Transfer Impedance (Zt), introduced by S. Schelkunoff in 1934, is a very convenient parameter for the prediction and control of EMI coupling through cable shields. Although widely applied to coaxial cables against EMI susceptibility problems, the Zt parameter can be easily extended to coaxial cables EMI emissions problems, as well as to Shielded Twisted Pairs (STP). This latter is more specifically addressed here, through the concept of Differential Transfer Impedance (Ztd).
I. BRUSH-UP ON TRANSFER IMPEDANCE Zt
Until a few decades ago, the Shielding Effectiveness (SE) of a cable was defined more or less in the same manner as for a Faraday cage or any shielded enclosure, as the ratio of the E (or H) field outside to the E (or H) field inside. More exactly, the field that would exist at a given point if the shield was not there, to the remaining field when the shield is in place.
In practice, with a shielded cable, the effects of the incident field are measured instead: that is the voltage (or current) induced on an unshielded wire illuminated by a given field, to the voltage (or current) on a shielded version of a similar conductor.
Although the principle looks sound and simple, providing a SE figure in dB, the measurement itself is not so easy, requiring the making of a strong electromagnetic field, hence a set of RF amplifiers and antennas, in a shielded—preferably anechoic—room. Like any radiated EMC measurement, it is plagued with a substantial uncertainty (typ. 6 dB), aggravated by the fact that below 50MHz, for 1m antenna distance, the test falls in near-field conditions. In such case, the measured SE will depend on the type of antenna being used : E-field illumination will give flattering results, while H-field (loop antenna) will produce overly severe results. Furthermore, test variables like the cable height and its terminating resistors are introducing poorly controlled effects.
In summary, the SE of a same sample, measured by a radiated method could vary widely from one test configuration to another, leaving the user with a SE figure which may not be transposable to his specific application.
Instead of an SE figure which is installation-dependent, the EMC Community has, since long, privileged a parameter that is intrinsic to the cable shield and to nothing else. This is accomplished by the Transfer Impedance (Zt), a brilliant concept introduced by Schelkunoff around 1934-38[1].
The transfer impedance relates the current flowing on a shield surface to the voltage it develops on the other side of this surface. This voltage is due to a current coupling through the shield thickness (if the shield is a solid tube, this diffusion rapidly becomes unmeasurable, due to skin effect, as frequency increases) and to the leakage inductance through the braid’s holes. The better the quality of the braid, the less the longitudinal shield’s voltage.
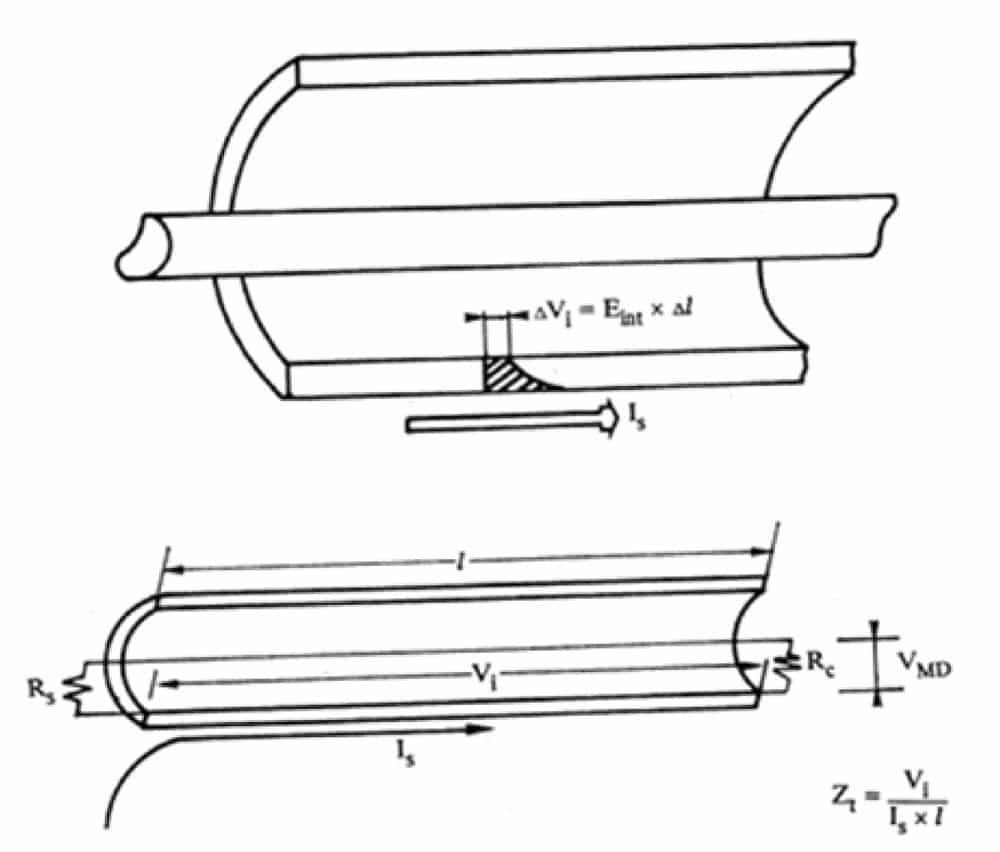
Zt is easy to measure, using a conducted injection set-up, less prone to errors and inaccuracies than a radiated test. A current (Figure 1) is forced on the shield by a generator or current clamp inserted in the cable-to-ground loop. Because of shield imperfections (shield resistance and braiding interstices) a small voltage appears in the inner space between the center conductor and the shield. This voltage, or a fraction of it, is measured at the end of the cable, connected to a Spectrum Analyzer or Oscilloscope input.
The result is normalized to a 1 meter long sample, such as:
Zt (Ω/m) = Vi (Volt) / (Ish x l m) (1)
where
Vi = longitudinal voltage induced inside the shield over length « l », causing a noise current to circulate in the center conductor
Ish = external current injected into the shield by the EMI source
If the cable is terminated at both ends in loads RL matched to its characteristic impedance, each end takes one half of the full induced voltage Vi. Finally:
Zt (Ω/m) = 2 x VL / ( Ish x lm )
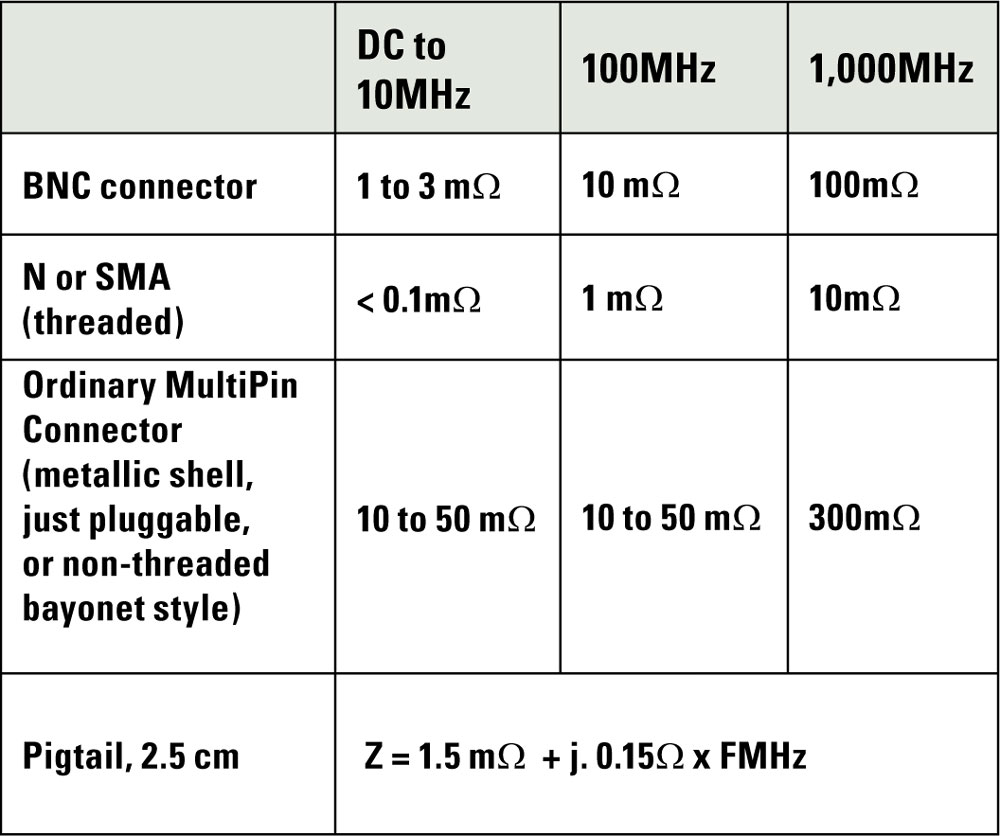
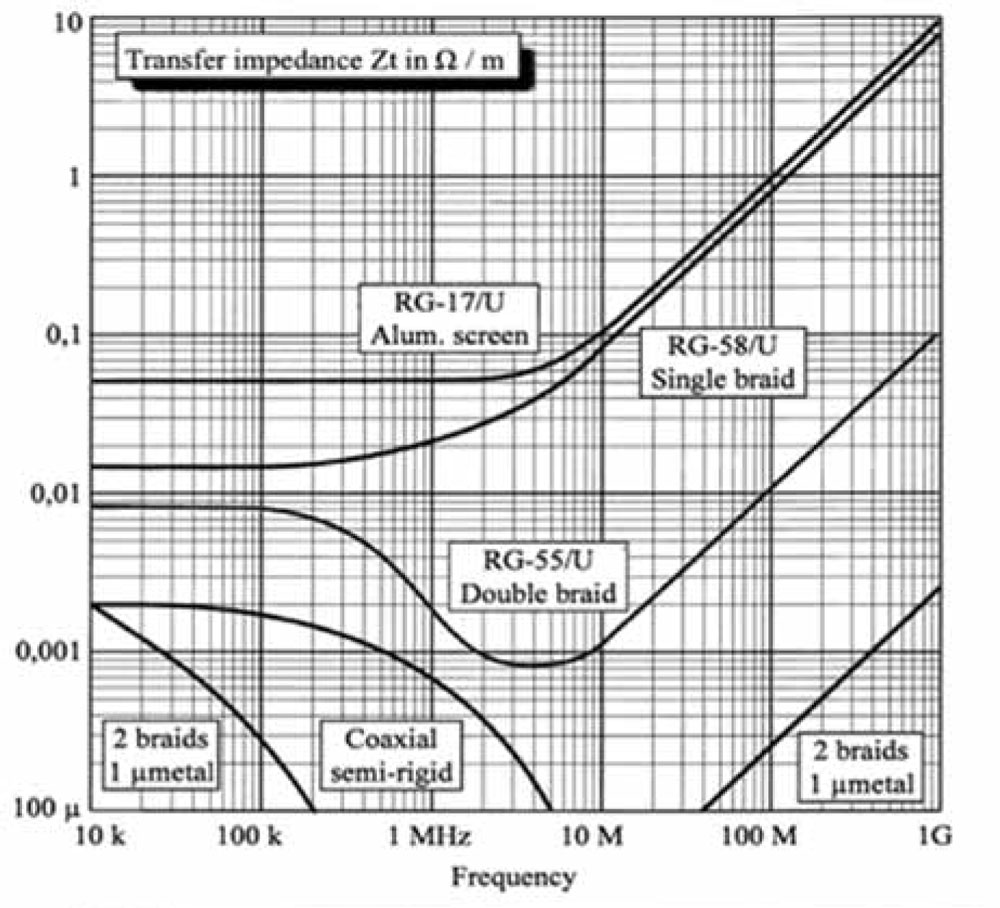
Typical values of Zt for various coaxial cables are shown in Figure 2. If the shield is grounded by pigtails (a poor practice) the pigtails impedances must be added to Zt, and to the loop impedance calculations. Below about 100kHz, Zt remains constant, being merely the shield’s ohmic resistance. Above 1 MHz, typically for a single braid, Zt increases with frequency, due to the leakage inductance Lt between the overall braid and the inner conductor. For a good single layer braid, Lt ranges around 1nH /m.
So, Zt can be expressed in the frequency domain as:
Zt (Ω/m) = Rsh (Ω/m) + j ωLt (Henry/m)
II. USING Zt IN SUSCEPTIBILITY PREDICTION FOR A COAXIAL CABLE
Initially, Zt was conceived for susceptibility calculations against a known EMI threat, for instance an ambient field illuminating the cable-to-ground loop area. The impedance of this external loop, for a single-braid coaxial with an outer diameter in the 5 to 15 mm range, and at a height of 50 to 500 mm above ground can be approximated by:
Zext = ( 10 mΩ + j 5 Ω x FMHz) per meter length (2)
If the field-to-loop induced voltage is known, this ground-loop impedance can be used to calculate the loop current Ish circulating on the shield. Knowing Ish, Zt can then be used straightforward to estimate the voltage appearing inside the shield:
Vi = (Zt x lm) x Ish (3)
If the EMI frequency is such as the cable length exceeds λ/2, then the physical length « l » should be replaced by λ/2 in the bracket term of Equation 3.
Example 1:
A 4m single braid coaxial cable, installed 0.75m above ground, is illuminated by an ambient RF field of 10V/m @ 15MHz, causing 9V of open loop induced voltage. What is the voltage appearing at the receiver end of the cable?
External loop impedance, calculated by Equation 2:
Zext = (0.01 + j 5 x 15 MHz) x 4m = 300Ω
The calculated loop current is:
Ish = 9V / 300Ω = 0.03A
For a single braid coax. like RG58, Figure 2 indicates Zt @ 15MHz = 0.15Ω/m.
The induced voltage on the coax center conductor is:
Vi = Zt x l m x I = 0.15 x 4 x 0.03 = 18mV
Assuming that the cable is terminated in 50Ω both ends,
VL = 18mV x 50 / (50 + 50) = 9mV
If the receiving endwas terminated in a high impedance, like 5kΩ:
VL = 18mV x 5000 / (5000 + 50) ≈ 18mV
Incidentally, one could grade the reduction factor gained via the shield as the ratio of the loop bulk voltage to the voltage appearing internally:
Kr = 9V / 18.10-3 V = 500, that is 54dB
III. USING Zt FOR PREDICTING RADIATED RF EMISSIONS FROM A COAXIAL CABLE
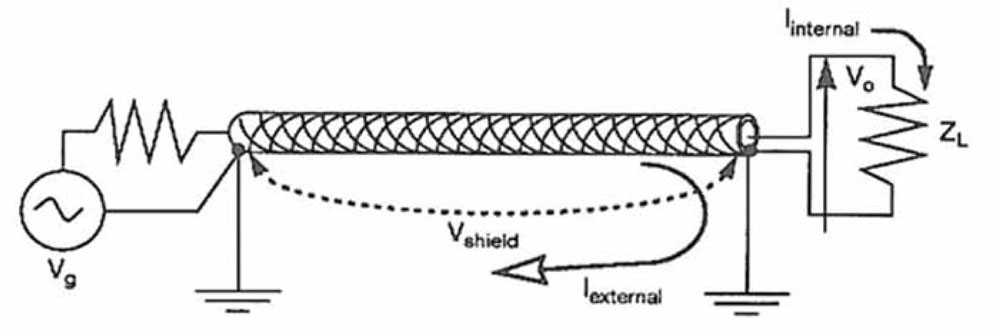
The principle of Zt is perfectly reciprocal and can be applied to emissions as well. RF signals, baseband video, some LAN links and other high-frequency signals are carried over coaxial cables. A very small fraction of the intentional signal current (typically 0.3 to 0.1 percent above a few MHz) returns by paths other than the shield itself (Figure 3). This assumes that the shield is at least correctly tied to the ground references at both ends, and preferably also to the chassis by the coaxial connectors.
The signal current I0 returning by the shield’s inner side is causing an EMI voltage to appear along the outer side. This voltage is given by:
Vext = Zt (Ω/m) x l (m) x I0 (4)
= Zt (Ω/m) x l (m) x V0 / ZL
In turn, this voltage Vext is causing an external current to excite the antenna formed by the cable-to-ground loop, hence radiating a small field that can be associated with the quality of the shield and its installation.
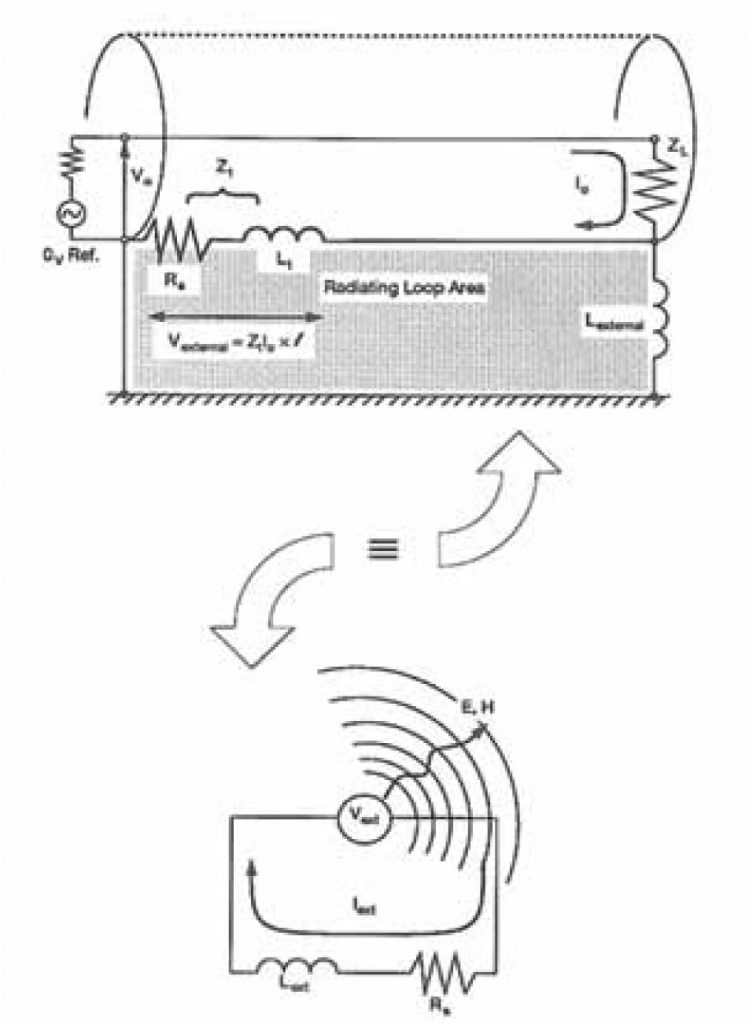
For estimating the E and H field from this low-impedance loop (see Figure 4), the external shield current can be found by:
Iext = Vext / Zext
where Zext is the same as the one calculated for susceptibility case. Eventually, pigtail or connector impedances have to be incorporated into Zext. Although their contribution to Zext is usually minimal, they can seriously deteriorate the shield transfer impedance, since Zt must be hundreds or thousands of times smaller than Zext, for a good shield.
If the shield is floated from the chassis, the shield becomes an electrically driven radiator. The radiated field can be calculated using monopole or dipole equations, with Vext, as an input.
When the cable becomes electrically long, Zt (Ω/m) no longer can be multiplied by the length, since the current is not uniform along the cable shield. A default approximation is to consider that the maximum amplitudes of the shield voltages distributed along the shield are:
Vext (max) = Iext. Zt (Ω/m) x λ/2 (5)
So, as Zt increases with frequency, the effective length which multiplies Zt decreases with frequency. At the same time, the cable-to-ground external impedance needs to be replaced by ZC, the corresponding characteristic impedance, using the following formula:
ZC = 60 logn (4h/d) (6)
Example 2
A two-meter piece of RG-58 coax is connecting two cabinets, with BNC connectors at both ends. The electrical parameters are:
Useful signal: 15 MHz video
Load resistance: 75Ω
V0 spectrum amplitudes:
fundamental (15MHz) = 10 Vpk
harmonic #3 ( 45MHz) = 3.3 Vpk
harmonic #5 ( 75MHz) = 2 Vpk
The geometry is:
Cable diameter= 0.5 cm, height above ground = 30 cm
Calculate the radiated field at 3 m due to harmonic #3.
Solution
First, we need to determine the area of the radiating loop:
A = 2 m x 0.3 m = 0.6 m2 = 6,000 cm2
For 45MHz, λ = 6.70m, so the 2m length of cable is already exceeding λ/4 , approaching λ/2. We can consider that the radiation efficiency of the antenna formed by the shield-to-ground loop has reached its maximum asymptote.
For a same reason, the external loop impedance is approaching its maximum, that is the characteristic impedance:
ZC = 60 log n (4 x 30 / 5) = 330 Ω
The internal signal current returning by the shield is:
I0 (45MHz) = V0 /75 Ω = 3.3 / 75 = 44mA
The external shield voltage, due to transfer impedance Zt is:
Vext (45MHz) = I0. Zt(Ω/m) x 2m,
where Zt (45MHz) is given by Figure 2 = 0,4 Ω/m
Vext = 44.10-3 . 0.4 . 2m = 35. 10-3 V
This voltage, in turn, is driving an external current onto the loop:
Iext = Vext / ZC = 35. 10-3 V / 330Ω = 107.10-6A
From this current, the radiated field at 3 m (far field conditions) can be quickly estimated [2] by :
E (µV/m) = [ 1.3 . Acm2 . Iamp . F(MHz) 2 ] 1/D
E (µV/m) = 560 µV/m , or 55dBµV/m
(*Note: Since the whole calculation has been carried in peak values, 3dB should be subtracted for peak-to-rms conversion, but they are apprximately offset by the ground plane reflection of the CISPR/FCC test set-up.)
Although this radiated level is about 500 times lower than if a bare wire were carrying the same current with a return by the ground plane, FCC Class B limit is exceeded by 15 dB @ 45MHz, with other limit violations at 75, 105 MHz and so on.
Several possibilities exist to reduce the radiated field:
- Select a coaxial cable with a lower Zt, like “optimized” braided shields (thicker, denser braid) or double-braid shield.
- Slip a large ferrite bead over the cable shield. It will take an added series impedance of about 1,200Ω to achieve the required attenuation, for instance passing the cable twice into a large ferrite toroïd.
- Reduce the cable height above ground.
IV. IMPORTANCE OF THE SHIELD CONNECTIONS
As important as a shield with low Zt is its low-impedance termination to the equipment metal boxes. The connection by which the shield itself is grounded to the equipment box (or PCB) has its own impedance, too.
This impedance consist of the shield-to-backshell contact, the connector-to-receptacle impedance (that may include some seam leakage inductance) and the receptacle-to-chassis contact resistance.
This connection impedance Zct is directly in the signal current return path, in series with Zt. Therefore, Zct can increase seriously the voltage Vext, which excites the
cable-to-ground radiating loop. At contrast with cable shield Zt which is a distributed parameter (Ω/m), Zct is a localized element.
Of course, if the shield is grounded by a piece of wire, or « pigtail » (a very poor practice), the connecting impedance is simply the self-inductance of this wire tail.
The following Table values can be taken for typical impedances of one single shield connection:
V. THE DIFFERENTIAL TRANSFER IMPEDANCE (Ztd) WITH SHIELDED PAIRS OR MULTICONDUCTOR CABLES
The concept of transfer impedance, used for radiated susceptibility or emission modeling of a coaxial cable, is transposable to shielded twisted pairs (STP). However, there is a noticeable difference: the shield is no longer an active return conductor.
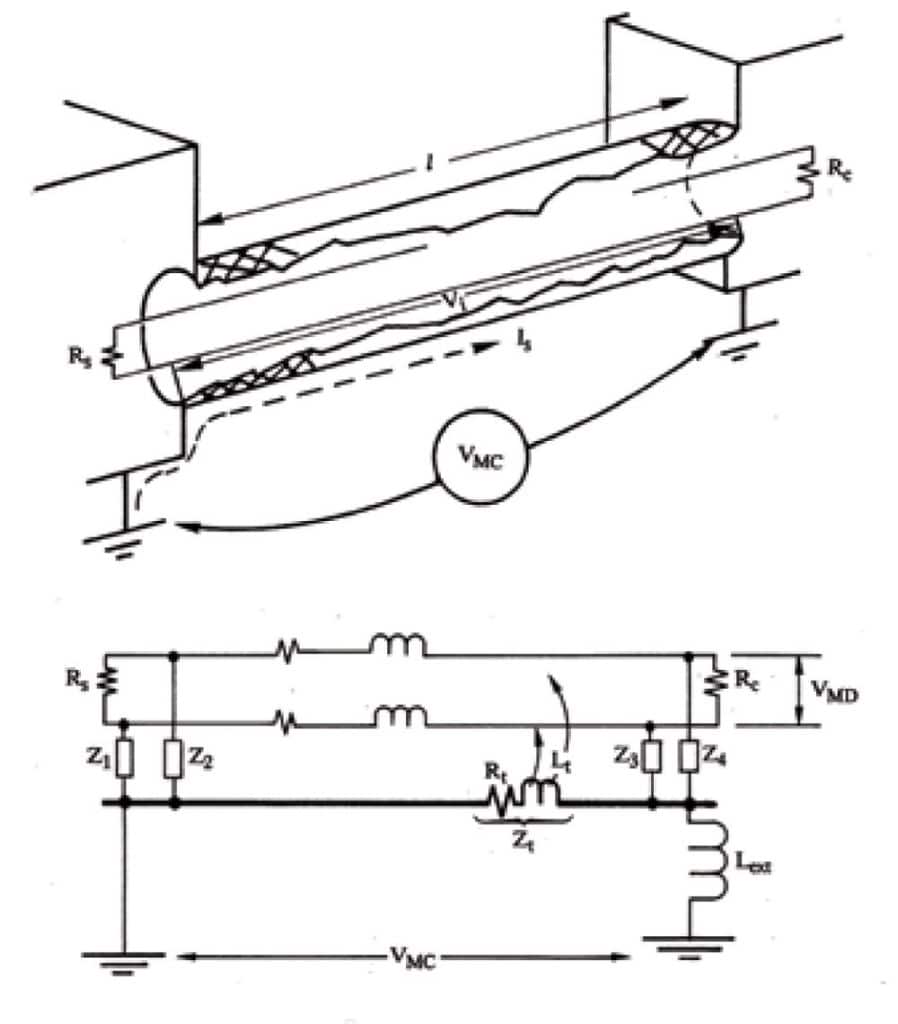
5.1 Susceptibility Prediction Using Ztd for a Shielded Pair
The induced voltage Vi appearing in the shield (see Figure 5) due to the loop current is not directly seen as a differential voltage across the wire pair. Two situations may arise:
a) General case
If the link is a true balanced one, using differential drivers / receivers and wire pairs, we can start from the voltage Vi appearing inside the shield due to the loop induced current Ish (see Equation 3).
Each wire 1 and 2 is exposed to the same voltage Vi, such as if the symmetry was perfect, the difference Vi(1) – Vi(2) would be null. Since there is a certain percentage of unbalance in the wires resistances, capacitance to shield and leakage inductance vs the shield, the differential voltage will be :
Vdm = Vi . X% . RL / (Rs + RL)
where X% is the unbalance percentage of the pair. Depending on the quality of the balanced link, X may range anywhere from 1 to 10 percent, with typical (default) value being 5 percent, for high speed data links.
Thus, replacing Vi by its expression for a coaxial cable configuration, we get:
Vdm = [Zt (Ω/m). l (m). I sh] . X% (RL/ (Rs + RL)) (7)
We can therefore define a Differential Transfer Impedance Ztd that will include the shield Zt times the pair unbalance, augmented eventually by the shielded connector Ztc and its own unbalance ( the contacts balance vs the metallic connector shell is not perfect either and can deteriorate the whole link symmetry). This new parameter Ztd will allow a single pass calculation of Vdm, from a given sheath current.
b) Case of unbalanced links using a STP.
If the associated Transmitter // Receiver circuits are of the unbalanced type (single-ended), without Bal.to. Unbal. conversion devices, one wire of the pair will be tied to the 0V reference at both ends and the whole STP behaves as a pseudo-coaxial link. The only small advantage being that the return wire dc resistance is paralleling the cable shield, or that the Electronic Reference ( 0V) could be eventually floated from chassis, yet the shield being chassis-grounded.
Example 3
A high speed differential link is using a STP, with following parameters:
LVDS Receiver: differential detection threshold: 100mV
STP: 0.80m long, good quality braided shield, pair unbalance ratio: 5%
System EMC specifications require a Bulk Cable Injection (BCI) test: 200mA rms, 30MHz – 200MHz
What will be the differential voltage seen at the receiving end?
Solution
Calculations are carried at 100MHz, which is about the worst case frequency region for 0.80m cable length.
1) Zt for a single braid @ 100MHz (Figure 2): 1Ω /m
Corresponding Ztd for 5% unbalance : 5.10-2 Ω /m
Vdm for 0.80m cable ( Equ.7) : Vdm = 0.80 . 1 Ω /m. 5.10-2 x 200mA = 8 mVrms
Since fast digital circuits (receivers, comparators) tend to respond to the peak value of modulated RF, the actual EMI voltage will be:
Vdm = 8.√2 = 11 mV, augmented eventually by a modulation coefficient.
Thus, based on shield coupling alone, the received voltage is 20dB below the LVDS detection threshold
2) The STP is terminated by plastic RJ45 plugs, with the shield grounded both ends via 12.5mm ( 0.5’’) pigtails. What is the new value of Vdm?
The total self-inductance for two pigtails ( typ. value 1nH/mm) is:
Lp = 2 x 12.5 x 1nH = 25nH
Corresponding parasitic impedance added in series to Zt, at 100MHz:
Zp = Lω = 16Ω
New value of Vdm, with the contribution of 2 pigtails (taking into account a same 5% unbal. as for the pair)
Vdm = [(0.80 . 1 Ω /m . 5.10-2) + 16 . 5.10-2] x 200mA = 170 mVrms, or 235 mVpk
This is more than twice (6dB) the LVDS detection threshold. The pigtails have deteriorated the transfer impedance of a fairly good braid by more than 20 times ( 26 dB). Metallic connectors insuring an integral shield grounding are necessary.
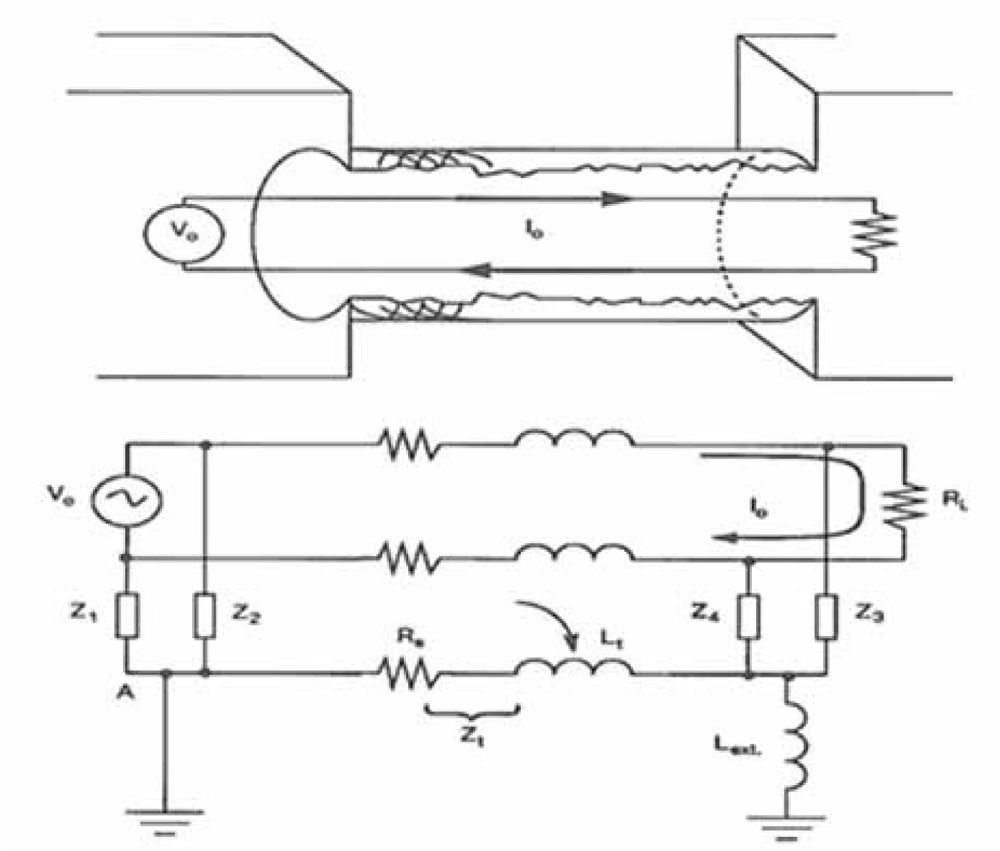
5.2 Application of Ztd to an EMI Radiated Emission Case
With true differential links using differential drivers / receivers and wire pairs, the current returning by the shield is only prorated to the percentage of asymmetry in the pair. If the transmission link is balanced with X percent tolerance, the unwanted share of current returning by the shield is, for the worst possible combination of tolerances, only X% of the total current.
In this case, Equation 4 becomes:
Vext = X% . Zt (Ω/m) x l (m) x V0 / Z L (8)
Thus, the radiated field is reduced by a factor equal to X percent, compared to a coaxial cable situation.
To the contrary, if the wire pair is interfacing circuits that are not balanced (e.g., the signal returns being grounded at both ends), a larger portion of the signal current will use the shield as a fortuitous return, like with case 4.1.b). This portion is difficult to predict. At worst, this unbalanced configuration cannot radiate more than the coaxial case.
Example 4
Using the same high speed differential link as example 3, calculate the field radiated at 3m by the fundamental component of a 100MHz data stream, with following parameters:
LVDS Driver , maximum differential output: 1000mV
100 Ω STP : 0.80m long, good quality copper braid shield unbalance ratio: 5%
cable diameter= 0.5 cm
height above ground = 75 cm
Solution
100MHz fundamental voltage, using usual Fourier series formulas for 50% duty cycle:
1000 mVolt x 2/ π = 640mV
Differential current, assuming matched load at receiving end:
640mV / 100Ω = 6.4mA
Corresponding shield external voltage, using Ztd (Ztd is taken from
example 3 @ 100MHz):
Vext = Id . Ztd x lm = 6.4. 10-3 (1 Ω /m . 5.10-2 x 0.8m ) = 260. 10-6 V
Characteristic impedance Zc of the cable, 75cm above ground:
Zc = 60 Logn (4.h/d) = 60 Logn (4 x 75 /0.5) = 380Ω
External current driven into the cable-to-ground loop by Vext:
Iext = V ext / Zc = 0.7.10-6 A
Loop area = 80 x 75 = 6000 cm2
Radiated field at 3m ( see Example 2)
E (µV/m) = [ 1.3 . Acm2 . Iamp . F(MHz) 2 ] 1/D
E (µV/m) = 18 µV/m, or 25 dBµV/m
This is about 22 dB below the FCC Class B limit.
If the shield grounding was made by the same pigtails as example 3, their deterioration of Ztd would raise the field to 380 µV/m ( 51.5 dBµV/m) exceeding the limit by 5 dB.
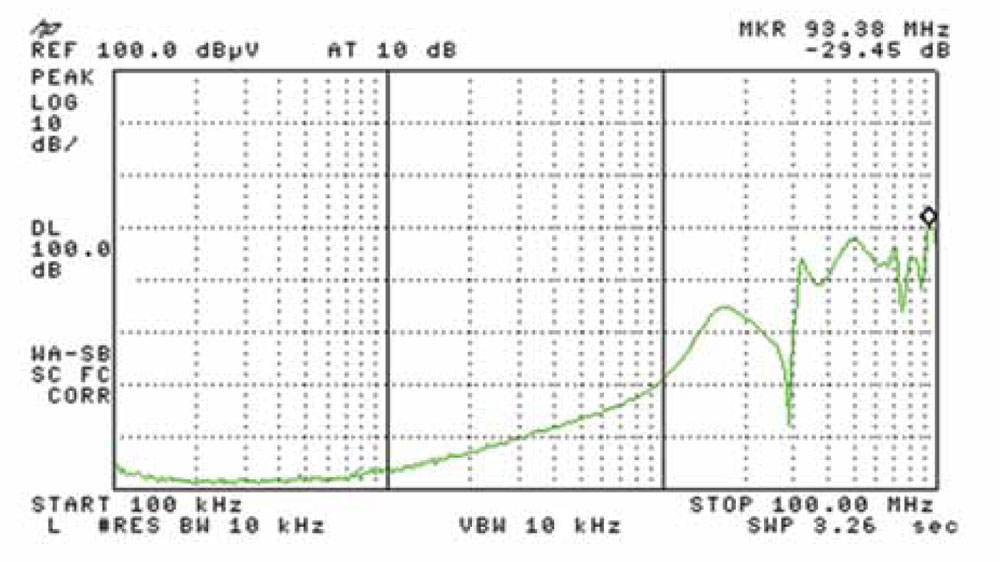
VI. ACTUAL MEASUREMENTS RESULTS WITH GOOD QUALITY ETHERNET STP
Figure 5 shows an example of unbalance measurements on an Ethernet type STP. Such measurements require a rigorous instrumentation set-up to prevent parasitic effects from obscuring the results. For instance, the Balun transformer, converting the symetrical 100Ω outpout to the unbalanced 50Ω input of the Spectrum Analyzer, must have at least a balance 14 dB better than the best pair being evaluated. This would just grant a < 2dB uncertainty of the results.
REFERENCES
- [1]. Schelkunoff, S. Electromagnetic Theory of coaxial lines and cylindrical shells, Bell Syst. Technical Journal, 1934
- [2]. Mardiguian, M. Controlling Radiated Emissions by Design, 2nd Edition, Kluwer Academics, 2001
Michel Mardiguian, IEEE Senior Member, graduated electrical engineer BSEE, MSEE, born in Paris, 1941. After military service in the French Air Force, worked for Dassault Aviation, 1965 to1968. Moved to the IBM R&D Lab. near Nice, France, working in the packaging of modems and digital PABXs.