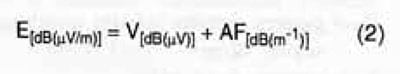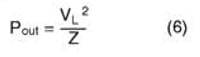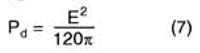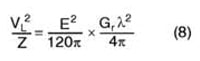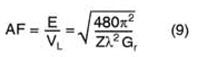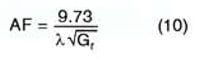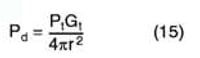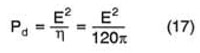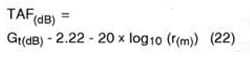*originally published in June 1997.
Introduction
The basics of the EMC profession often get buried under the day-to-day effort of continuous measurement and the volume of test and reporting paperwork. The fundamental parameter of the most common of technical tools, the EMC antenna, is used over and over without thought as to its actual meaning. This parameter is the antenna factor (AF). A review of the basics behind this parameter, and a related parameter, the transmit antenna factor (TAF), provides a basis for the use of the numerical values, and a more fundamental understanding of radiated EMC measurements.
EMC Antennas
EMC antennas are used for EMC measurements in rather rugged environments involving frequent handling, rapid replacement with a different antenna for another frequency band and the normal wear and tear of day-in, day-out usage, two shifts a day, six days a week, in almost all weather conditions.
For all their apparent simplicity, antennas used in an electromagnetic compatibility (EMC) laboratory are as specialized and as sophisticated as antennas for any other application. These antennas are different in that their application makes broad bandwidths the most important design parameter, and gain, efficiency, and low input voltage standing wave ratio (VSWR) become secondary. Broad bandwidths are driven by the broad frequency spectrum covered in the performance of EMC radiated emission and immunity measurements.
The antenna parameters that are familiar to most antenna designers are then secondary design objectives in the development of these antennas. For all the importance of the bandwidth, however, the antenna parameter most often used, the AF, does relate to the performance of the antenna. The AF is used to quantify the value of incident electric fields, and its companion parameter, the TAF, is used to determine the value of the electric field at a known distance from the generating antenna.
EMC antennas are used for two types of measurements: radiated emissions (RE) and radiated immunity (RI). In the first case, formal calibration of the antenna and the use of traceable standards are required. In the second case, calibration is not required as the calibrations are usually performed as part of a complete EMC test setup. Each of these types of measurements employs a separate descriptive parameter. For radiated emissions measurements, the parameter is the AF. For radiated immunity or susceptibility measurements, it is the TAF.
These two parameters are illustrated in Figure 1. This figure also illustrates other relationships between parameters used in the following derivations.
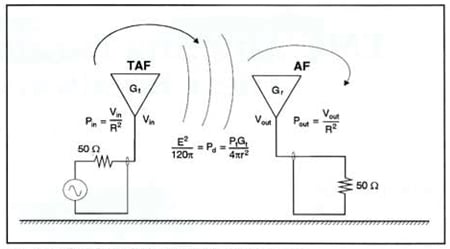
Antenna Factor
The antenna factor is the term applied in radiated emissions testing to convert a voltage level fed by a transducer to the input terminals of an EMI analyzer into the field-strength units of the electromagnetic field producing that voltage.1 It relates the value of the incident electric or electromagnetic field to the voltage at the output of the antenna. For an electric field antenna, this is expressed as
where
AF = antenna factor, m-1
E = electric field, V/m
VL = voltage at antenna terminals, V
The AF is usually expressed in dB and when used to determine the value of an incident electric field, the expression is:
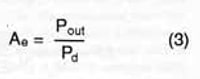
The derivation of the AF is straightforward and is based on several fundamental relationships in antenna theory. The relationships can be stated as: The ratio of power in the terminating resistance to the power density of the incident wave is defined as the effective aperture.2
Thus:
where
Ae = effective receiving antenna, m2
Pout = power delivered by antenna, W
Pd = power density of the incident wave, W/m2
Following this, then:
In addition, from the ITT Handbook3
where
Gr = gain of the receiving antenna wavelength, m
The output voltage from the antenna VL and the output power are related by the impedance seen by the antenna.
where
Pout = power delivered at the output of the antenna, W
VL = output voltage, V
Z = load impedance of the device connected to the antenna, Ω
Finally, the relationship between electric field strength and power density of the incident and the electric field strength is
where
Pd = power density of the incident wave, W/m2
E = electric field, V/m
Substituting Equations (4), (5) and (6) into Equation (7), gives, for a plane wave
Solving for the AF gives
In a 50-ohm system this becomes
In dBs, this becomes (in units of inverse meters)
Transmit Antenna Factor
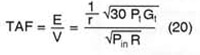
The TAF provides a means of computation of the input voltage to the antenna to provide a given value of electric or electromagnetic field at a stated distance from the antenna. The transmit antenna factor relates the value of the electric or electromagnetic field generated by an antenna as a function of its input. Thus, the fundamental relationship is
The transmit antenna factor is, then, expressed in terms of dB:
or:
Derivation of the TAF proceeds from three standard relationships. The first is a variation of the Friss transmission formula4.
where
Pd = radiated power density at distance r from the antenna, W/m2
Pt = power input to the antenna, W
Gt = numerical gain of the antenna
r = distance from the antenna where the power density is evaluated, m
The second is Ohm’s Law5
where
P = power dissipated in a load, w
voltage across the dissipating element, V
R = resistance (impedance) of dissipating element or load, Ω
The third relationship is Ohm’s Law for Free Space6
where
Pd = power density of the incident wave, W/m2
E = electric field strength at that point in space, V/m
n = impedance of free space,= 377πΩ WΩ
Combining Equations (14) and (16) leads to a familiar expression
which relates the electric field strength at a point r away from the transmitting antenna having input power Pt and gain Gt.
By rearranging Equation (15) we have:
Recalling the definition of the transmit antenna factor, the ratio of the E-field developed to the input voltage to the antenna, we can find the TAF by taking the ration of the E-field produced from Equation (17) to the power dissipated in the antenna given in Equation (18)
Remembering that the transmitted power Pt is identical to the power dissipated in the load, Pin, and R is 50 W, Equation (19) simplifies to
This result is reasonable, as the TAF should be an inverse function of distance from the source, and a direct function of the gain of the transmitting antenna, and should be independent of power input. It should be noted that the gain value in Equation (17) is the effective gain of the antenna, calculated from the measured values of the AF. The TAF as used above incorporates antenna efficiency, the effect of antenna mismatch and other losses.
The TAF expression can be converted to dB form by taking 20 x log10 of both sides of Equation (20). This gives
Note that the TAF is proportional to the gain of the antenna and inversely proportional to the distance from the antenna. This is rational and suggests that the derivation is correct.
Conversion Between AF and TAF
As can be seen from the derivations, although the AF and TAF have the same units, m-1, they are neither identical nor reciprocal. They are connected for both expressions. This fact allows the TAF to be computed from the AF by recalling that fM = c, and rewriting Equation (11) as
Substituting Equation (22) for Equation (23) gives
This conversion is valid for the conditions from which either the AF or TAF is measured. If the AF is measured over a ground plane (typical condition), then the TAF computed from the AF is valid for a similar condition.
Remember that the concept of reciprocity, as it applies to antennas, relates to the transmit and receive pattern. As such, the reciprocity does not include the effects of impedance mismatch, efficiency or other factors. These factors are included in the measured AF. Thus, if measured antenna factors are used, the TAF computed from these values will be accurate when the antenna is used under the same conditions, over a ground plane. A semi-anechoic chamber also fulfills the same conditions, subject to the constraint that, over the frequency range of the application of this concept, the RF absorber must be effective.
Summary
The above discussions have provided simple derivations of two parameters of an EMC antenna the AF and the TAF. These parameters are in daily use by many, but the source of the values is not well known. It is the purpose of this paper to provide the derivations of these parameters to illustrate the use of antennas and why they work as they do.
Acknowledgements
The author wishes to express appreciation to Edwin L. Bronaugh of EdB Consultants for technical input and reviews of portions of this paper, and to Dr. Thomas Chesworth of Electromagnetic News Report for permission to incorporate portions of a previously published discussion of TAF in this article.
References
1. Edwin L. Bronaugh and William S. Lambdin, Electromagnetic Interference Test Methodology and Procedures, Volume 6, A Handbook Series on Electromagnetic Interference and Compatibility (Gainesville, Virginia: Interference Control Technologies, 1988), p. 2.50.
2. John D. Kraus, Antennas (New York: McGraw-Hill Book Company, 1950), p. 43.
3. Reference Data for Radio Engineers, 6th Edition (Indianapolis: Howard W. Sams & Co., Inc, 1975), p. 27-8.
4. Kraus, p. 54.
5. N. Blabanian, Fundamentals of Circuit Theory (Boston: Allyn and Bacon, Inc., 1961), p. 13.
6. Kraus, p. 136.
JOHN OSBURN is the principal EMC scientist for EMC Test Systems. He is a member of the IEEE EMC Society and the Society of automotive Engineers, and is an active participant in EMC standards development for ANSI, the IEEE and SAE. John has thirty years experience as a lead EMC engineer, and has worked on projects ranging from single equipment to major systems with operating frequencies from 3000 sec/cycle to 34 GHz. He graduated from the University of Texas in Austin with a BSEE and the University of Southern California with a MSSM in 1985. He is a NARTE-certified EMC engineer and the author of many technical papers and articles. (512) 835-4684, ext. 669.