Read other posts in the “Elephant in the Test Room” series here.
At the time of writing, I am waiting to see if borrowing 3D EM software is on the cards, so let’s postpone progress on Elephant #3 for the time being. I’m quite excited at the prospect of modeling the present automotive emissions test fixture, and equally important, modeling the proposed improvements. In the meantime, we can continue with the current live threads.
The Cell-Phone Threat
The 3G (WCDMA) Transmitted Waveform
As previously explained, unique allocated orthogonal codes running at high speed (3.84 MHz) are used to spread each user’s narrowband data. This is shown in Figure 1. The horizontal colored lines at the output of the mixers are the spread-data ready for combination, frequency translation, amplification and finally, transmission. Again, as previously explained, each user’s data can be recovered from the composite transmitted signal by use of the user’s self-same unique orthogonal code.
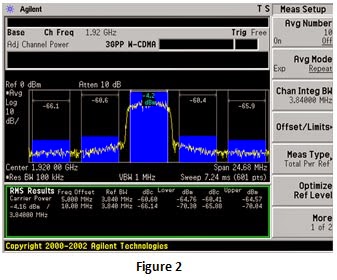
A screenshot of a real transmit signal amplified and ready to be fed to an antenna is shown in Figure 2 (the yellow trace). Clearly, this is an Agilent instrument, as is the waveform generator that created the test signal (WCDMA FDD Downlink Release 8, Test Model 1 + 16 DPCH). So, credit is due to Agilent for the screenshot.
The yellow trace doesn’t tell the entire story in that occasionally the codes phase align, creating very large peaks. A different plot (not shown) shows the percentage of time peaks of various heights occur.
When I was first acquainted with the linear amplification of WCDMA signals (I’m guessing around the year 2000), these occasional peaks were 13dB (20 times) above the average composite signal power, a tough requirement for the amplifier if information was not to be lost. If you think about it, for the information to reach the other end undistorted, the amplifier must be able to amplify the peaks, so you need an amplifier rated at the peak power. If the average power is 10W and the peak is 20 times this, you need a 200W amplifier. Strangely, web research today says that the peak to average is far lower. Maybe software clipping is employed as well as amplifier linearization.
Topical and timely for our purposes is the fact that Agilent is presenting a webinar on how the cell phone communicates with the base station when first setting up a call. This is when the cell phone is emitting at its worst in terms of the likelihood of interfering with nearby electronic equipment.
The title is “A day in the life of your cell phone” and the presenter is Darcy Smith, a field application engineer at Agilent.
Well, wouldn’t you know it? This clashes with an event given by Rohde & Schwartz that I am registered to attend. The R&S tutorial on “RF Back to Basics” takes place in Austin, TX and sounds pretty good. Guess I need to choose which one to attend, as I really wanted to ask Darcy questions on the latest cell phone peak and average powers when they are polling for the nearest base station. My guess is it is somewhere between 1.0 and 2.0 watts, but it would be good to hear it ‘from the horse’s mouth.”
The Linearization of EMC Amplifiers
Reminder: In the previous post on this thread, we asked the $64,000 question, “what is a practical level of harmonics in an RF immunity system?”
With commercial testing, the amount of the test field created by harmonics is limited by stipulating that the harmonic field must be at least 6 dB down from the field created by the fundamental. Applying limits on the make-up of the test field to maintain the integrity of the test field has to be the way to go, since it covers all the imperfections in all of the equipment used in generating the test field. To do otherwise is simply conjecture based on likely worst-case performance of all the components in the line-up, plus perhaps an arbitrary safety margin. Bear in mind that cables will attenuate the harmonic, while the antenna will likely favor it to some extent or other. But, some antennas are better than others. What if you invest in components that give performance way better than the supposed worst cases? What need of the automotive 1 percent maximum amplifier harmonics then?
So, we will stick with the eminently superior approach that frames the integrity of the test field itself. Right then, if the harmonic field is 6dB down from the fundamental field (i.e. minus 6dBc), what portion of the total test field is allowed to be created by the harmonic?
Easy enough to deduce, but long winded in terms of step-by-step. The total field created during commercial calibration is 18v/m (10v/m test level plus 8v/m to allow for the peak field created by the AM modulation). We put the harmonic content at its allowed limit of -6dBc.
We are talking v/m, so
-6 = 20 log10 [harmonic field / fundamental field]
-6/20 = log10 [harmonic field / fundamental field]
-0.3 = log10 [harmonic field / fundamental field]
antilog10 (-0.3) = [harmonic field / fundamental field]
[harmonic field / fundamental field] = 0.5
That is the fundamental field is twice the level of the harmonic field.
The total test field is 18 v/m = fundamental field + harmonic field.
But, we just stated the fundamental field is twice the harmonic field.
So, 18v/m = 2 x harmonic field + harmonic field,
which means that 18v/m = 3 x harmonic field.
The harmonic field is 6v/m, leaving 12v/m for the fundamental field.
So, the maximum portion created by the harmonic is one-third of the test field (I misstated this in a previous post, sorry).
Just because we can, let’s apply this limit to automotive RF immunity testing. This means the prescribed 200v/m test field would be allowed to include up to 67v/m of harmonic field.
We established the dependence of the harmonic in the field E2 previously as:
To reinforce the fact that this is the level of the harmonic compared to the fundamental (the carrier, i.e. dBc), we will rename E2 as E2dBc
To find out the harmonic level from the amplifier when the harmonic field is -6dBc, we can make P2/P1 the subject of the equation.
For E2dBc = -6, the antilog10 [E2dBc/10] part is antilog10 -0.6 = 0.251
If we only knew the linear gain of the antenna at the fundamental and harmonic frequencies, we could complete the unknowns and establish the harmonic performance required from the amplifier, that is 10log10 [P2/P1].
A web search gives data on a typical 1-18 GHz antenna. I extended the data to create Table 1. It shows the harmonic gain next to the fundamental gain, and the delta between the two in dB.
A glance shows the worst case delta between a fundamental and its harmonic is at 8 GHz where the antenna gain at 8 GHz is 11 dBi and its gain at 16 GHz is 15 dBi.
The table shows the respective linear gains. Slotting these into the equation gives:
So, the harmonic performance from the amplifier is required to be -10dBc, a far, far cry from the automotive -20dBc.
I suppose if I wanted to alarm the automotive technical committee and insist amplifiers need to meet -20 dBc, I could say something like this:
“Data shows irrefutably that the low frequency antenna gain and the high frequency antenna gain can differ by more than 8dB, so harmonics must be kept extremely low.”
This is true in that the worst case between 1 GHz and 16 GHz is 15dBi minus 6.8dBi equaling 8.2dB. Pretty frightening but not representative of the actual worst case delta between any real life test frequency and its harmonic. Who cares that at 1 GHz, the gain is 6.8dBi and at 16 GHz, the gain is 15dBi. The two frequencies will not co-exist during testing. In fact, when the test frequency is 1 GHz, the delta between it and its harmonic (2 GHz) is only 1dB.
Personally, I’d double this minimum harmonic performance to -13dBc, partly as a safety margin, but in truth mainly because this is the performance of TWT amplifiers once they are past the first 20 percent of the band. Also, when it comes to our linearization exercise on improving the harmonics in the first 20 percent of the TWT amplifier band (can be as bad as minus 3dBc), an improvement of 10dB is not to be sniffed at. This is 10 times better and after all is said and done, when using one instrument to calibrate another, we are happy to insist the accuracy should be 10 times better than the instrument being calibrated.
-Tom Mullineaux