Author
Steven Weir
Abstract
While voltage regulator vendors often suggest generic filter capacitors for use with their devices, these recommendations are often both vague and fail to take into account the effects of the larger PDN bypass network on VRM response.
Filter Capacitor Networks
Figure 1 depicts a generic PDN conceptual model.

Moving from left to right we have: The the switching power stage for SMPS VRMs, the effective transfer function impedance of the VRM, bulk and bypass filter capacitor branches, series interconnect inductances, and finally a mounted IC load which may have its own internal capacitors.
PDN filter optimization consists of:
- Buying only the number of capacitors needed for high frequency performance.
- Buying only the number of Farads needed for low frequency performance.
- Inserting frequency compensation as needed for stable response.
PDN designs may be classified as tightly or loosely coupled through the effective frequency range of the VRM bulk capacitors. Tightly coupled designs are those where the interconnect impedance is small compared to the parallel equivalent impedance of the high frequency capacitors through the upper frequency response of the VRM. For most linear regulators the frequency limit is less than 1MHz. Most PCB PDNs particularly those with linear regulators are tightly coupled.
In tightly coupled designs, the distributed bypass network directly loads the VRM within the VRM’s closed loop response. The distributed high frequency capacitors provide capacitance that need not be duplicated by bulk capacitors, but also must be accounted for in the VRM error response.
Because the high frequency performance of the PDN constrains the quantity and value of most of the capacitors, VRM filter design actually begins by designing the high frequency network first. This network is then fitted to the VRM requirements.
All VRMs are at their heart feedback control systems. The PCB PDN and ICs load the output amplifier altering the closed-loop transfer function. The primary concern is to realize an unconditionally stable response that accounts for the high frequency bypass network, and any large in-package IC capacitance.
An unfortunate reality is that most linear regulator data sheets and application notes fail to numerically specify acceptable filter capacitor parameters. In many cases vendors only vaguely recommend generic capacitor types such as tantalum or aluminum electrolytic capacitors. Other times, vendors may state that there products are tolerant of low-ESR MLCC capacitors without much further elaboration. The following design procedure gets around this ambiguity by characterizing the VRM in simulation.
Design Procedure
- Add together the total PDN load capacitance as the parallel equivalent of all high frequency capacitors on the rail as well as any large IC in-package capacitance on the rail as CPDN.
- Determine the initial bulk filter capacitance: CBULK_INITIAL as the difference between the VRM manufacturer’s recommended bulk capacitance and CPDN.
- Select an MLCC, or where necessary for capacitance parallel MLCC capacitors that together equal or exceed CBULK_INITIAL.
- Perform transient simulation loading the VRM with the PDN network in parallel with CBULK_INITIAL.
- If the transient simulations show less than 1.5 cycles ringing, the design is stable. In cases where CBULK_INITIAL is costly as an MLCC, select a lower cost electrolytic capacitor as a substitute and resimulate. Otherwise, the MLCC form of CBULK_INITIAL is the final design choice.
If the transient simulations show more than 1.5 cycles ringing a dominant pole with ESR is required. The next task is to determine the pole values, and on that basis select a final bulk filter capacitor value.
Dominant Pole Compensator Synthesis
- Replace CBULK_INITIAL with an ideal capacitor CDP, and an ideal series resistor RDP.
- Set CDP to the smallest E3 value larger than 2*CPDN.
- Set RDP initially to 1mOhm.
- Interatively, repeat the transient simulation increasing the value of RDP by 1.4x steps until the transient ringing settles within 1.5 cycles.
- Select a suitable capacitor with a minimum ESR at least equal to RDP and no more than 4x RDP. Alternatively, a discrete resistor in the same range can be inserted in series with MLCC capacitor(s).
- Simulate the final selection.
Transient Simulation Set-Up
The transient simulation can be performed in any SPICE variant, including the free LT SPICE Linear Technology, or WebBench offered by TI/National.

The simulation evaluates load transient stability. It supplies the VRM from an ideal voltage source. A pulsed current source loads the VRM. Pulse width should be set to approximately match the VRM manufacturer’s data sheet test waveforms. However, pulse widths of 50us repeating at 100us are almost always adequate. Rise and fall times should be no more than: 1/(10 F0dB ), where F0dB is the 0dB intercept for load response if specified, or line rejection if load response is not specified. 100ns is generally adequate for all but the highest bandwidth linear regulators.
Design Example
For the design example we use a popular three terminal regulator: LT1083 from Linear Technology Inc. applied as a 3.3V regulator LTI recommends a 1uF frequency compensation capacitor and a 10uF unspecified tantalum capacitor for bulk filtering. Tantalum 10uF capacitors are available in different forms with ESRs from 25mOhms to 10 Ohms. The data sheet and application notes offer little further guidance. Insufficient ESR results in ringing and slow transient recovery. Excessive ESR results in excessive transient voltage excursions.
In our example the high frequency PDN is represented as 24 pieces of a major MLCC manufacturer’s 470nF 0402 X5R capacitor attached with nominal attachment inductance to the power planes. The 24 470nF capacitors together: CPDN exceed the 10uF manufacturer recommendation. We start without any bulk capacitor. The resulting transient response as seen in Figure 3 exhibits substantial ringing. We will need to add dominant pole compensation.

Following our procedure we first select an E3 capacitor value at least twice the parallel capacitance of the PDN. 22uF is adequate. Next we iterate transient simulation changing the ESR values until we adequately damp the transient ringing. We find that 32mOhms ESR is the minimum adequate ESR. As seen in Figure 4, the compensated response settles quickly with a nearly 50 percent reduction in peak excursion.
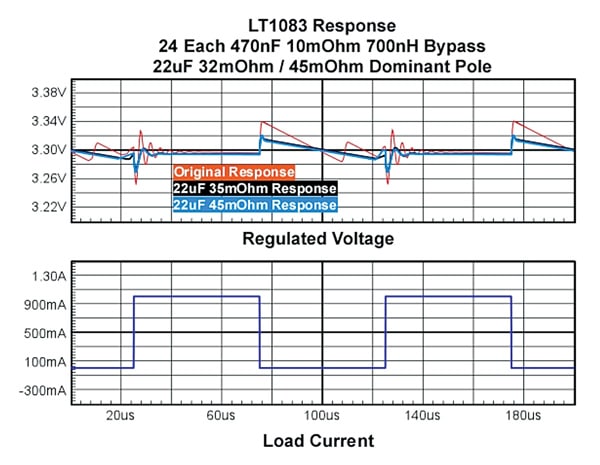
We can realize the dominant pole compensation network by several alternative capacitor choices:
A 22uF MLCC in series with a 35mOhm thick film resistor. Budgetary cost: $0.20
An aluminum polymer SMT capacitor 22uF 40mOhms. Budgetary cost: $0.45
A tantalum polymer SMT capacitor 22uF 40mOhms. Budgetary cost: $1.33
Summary
VRMs are fundamentally feedback control systems. When the interconnect impedance is low throughout the frequency response of the VRM, the entire PDN is tightly coupled to and loads the VRM, reducing the required bulk capacitance, but also potentially destabilizing the response.
Through a simple simulation driven procedures, optimal VRM response can be obtained while allowing the use of compact, low cost solutions.





