Read other posts in the “Elephant in the Test Room” series here.
Please note, regarding the fate of Elephant #2 – ‘Disharmony in Harmonic Limits’, it has now fallen under the umbrella of ‘Linearization of EMC Amplifiers’ and will be alluded to again during the part of the design exercise that determines practical harmonic levels.
And so, with no further ado, onto a whole new elephant…………
Elephant #3 – Fixing the Broken Automotive Emissions Test Fixture
The Room: Automotive RF Emissions Testing
The Elephant: Hard to justify systemic uncertainties
The Culprit: An over-reliance on weakly related historical methods compounded by the turning of a blind eye to known serious flaws
Note: It is important that we are all at the same place when we discuss this topic or you may be left behind, or find yourself pondering needlessly over points already covered in the recently published article ‘A Design Review of the Automotive Radiated Emissions Test Fixture’, so it will pay to read this first.
We start by describing a means of getting a feel for the present level of error when measuring the fields emitted by the wiring harness. The test currently relies on the 1m calibration data supplied with the biconical antenna.
Very simply, ten single frequency fields are emitted from the harness one at a time over 20-200MHz and a field probe is used to measure the field strength 1m away. The article already describes how the test fixture can be characterized with a signal generator providing a known spot frequency at a known injected power level.
The measurements are then repeated with the biconical antenna in place of the field probe. It is easy to convert the dBuV reading on the receiver back to the field the antenna ‘sees’ using the supplied calibration data.
Anyone out there have the facilities, time, and inclination to try this? For the purposes of this experiment we can probably devise a way of initially avoiding the need for a 50-300 Ohm transformer.
Before signing off until next time, I would estimate the figure for getting an independent RF house to review and fix the system as $30k-$50k. Even if it turned out to be twice or even three times that estimate, surely this pales into insignificance when compared to the cost, (financial and injury to reputation), of just one vehicle recall. You might think that the automotive manufacturers’ EMC departments would get their heads together and fund the project jointly. In my view, the various groups that presided over this debacle of a test set-up to date have demonstrated their ability already, and should be excluded from the project until the new fixture design has been proven.
To be continued…
Linearization of EMC Amplifiers
Homing in on the Phase Control
For optimum control of the harmonic cancellation process we need to be able to adjust the phase and amplitude of the cancelling signal. The amplitude control is comparatively simple as we can get the PC to change the output power of the signal generator as required. So for now we will concentrate on the phase control, but should bear in mind that any phase shifter we choose will be frequency dependent. That is the insertion loss of the shifter will increase with frequency, causing a reduction in signal amplitude. However this is of no great matter as we are designing a self monitoring / correcting system.
To make the objective we are seeking here perfectly clear, we will divorce our thinking from the job in hand and simply look at the output of two signal generators.
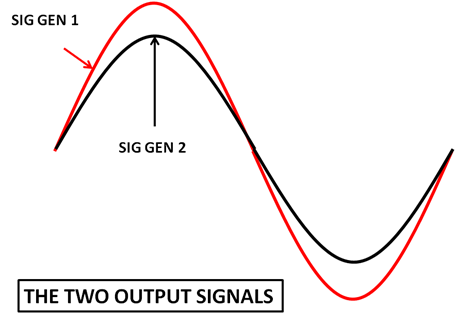
The generators are locked together by connecting the ‘sync’ connectors on the back panels and so will start in phase as shown in the first figure. The amplitudes are different only so we can see both signals when they coincide.
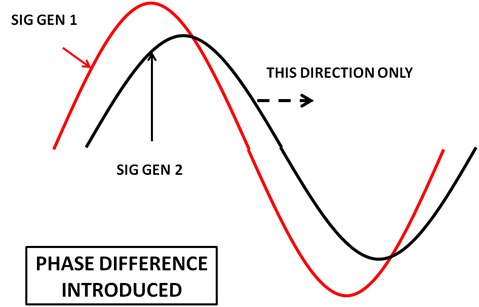
The second figure shows what happens when we introduce a phase shift (lengthen the electrical length of the second generator cable connection).
The phase shifter can only add electrical length to the output connection from the second signal generator and so, as shown, the black trace can only move to the right. This is a nuisance when to phase align the two signals we only need to move the black trace slightly to the left. So we will deliberately put a phase lag into the red trace. This way we can always get the two to align when we phase shift the black trace to the right. This is shown in the next figure.
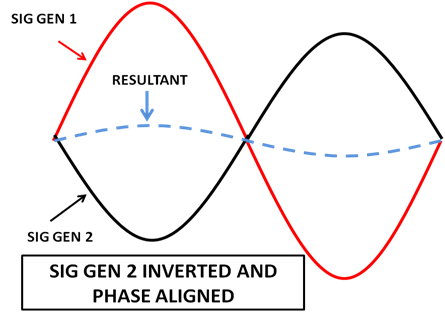
The final figure shows the resultant when we press the ‘invert’ button on the second signal generator and use the phase shifter to align the two signals.
The resultant is the only signal that will appear when the two outputs are combined.
Getting back to the job in hand, we must remember that the two signals we are talking about are signals at the output of the TWT amplifier. And so we must bear in mind that we do not as yet know the insertion phase of the TWT amplifier, so the offset lag (read the length of the line stretcher we will install) and which arm it needs to go in will need to be determined when we characterize the TWT amplifier.
To be continued….
The Cellphone Threat
In this post we complete the description on the 4G orthogonality concept, then in the next post we will move onto the 4G and 3G transmitted waveform characteristics.
4G (OFDMA) Orthogonal Codes Continued……
It was explained previously that OFDMA splits the very fast serial data to be sent into many parallel, far slower, frequency separated channels sent as a tightly packed spectrum. At the receive end the slow parallel data channels are converted back into the original fast serial data stream. The separation of each parallel channel from the ‘pack’ is achieved through the fact that a signal frequency multiplied by itself and integrated produces a non-zero result, whereas when this frequency is multiplied by any other frequency in the pack a zero result is produced. The figure below shows the concept.
The variable signal generator presents each ‘bin’ frequency in turn (f1 then f2 etc) and this is multiplied with the ‘pack’. To see why only the wanted signal produces a result when mixed with the correct bin frequency we need to revisit the high school trigonometric identities we were all forced to learn by rote.
Proof of a zero result when sinusoidal waveforms of different frequency are multiplied and integrated
From the trigonometric identity cos(u)cos(v) = ½[ cos(u-v) + cos(u+v)]
∫cos(u)cos(v)dt = ½ [∫cos(u-v)dt + ∫ cos(u+v)dt]
But the algebraic sum of the area under the curve of the cosine function over one cycle is 0, so
½[ ∫ cos(u-v)dt + ∫ cos(u+v)dt] = ½ [(0) + (0)] = 0
That was easy. Now for the next.
Proof of a non-zero result when a sinusoidal waveform is multiplied by itself and integrated
From the trigonometric identity cos(u)cos(v) = ½[ cos(u-v) + cos(u+v)]
And letting v = u
cos(u)cos(u) = ½[cos(u-u) + cos(u+u)]
cos2(u) = ½[cos(0) + cos(2u)]
cos2(u) = ½[1 + cos(2u)]
Again, the algebraic sum of the area of the cosine function over one cycle is 0, so
∫ cos2(u)dt = ½ ∫ [1dt + cos(2u)dt] = ½T + ½ (0)
= ½T, where T is the time to complete one cycle
And that completes the basic concept behind 4G OFDMA.
Next time we will look at the transmitted waveform characteristic.
To be continued ……
-Tom Mullineaux
Previous posts in the Elephant in the Test Room Series:
1. Elephants in the Test Room
2. Elephants in the Test Room #1 Continued – Further Expansion on the Culprit
3. Elephant in the Test Room #1 Continued – How Other EMC Sectors Dealt with the Elephant
4. Elephant in the Test Room #1 Continued – The “Money No Object” Approach to Fixing the Under-Test Situation
5. Elephant in the Test Room #1 Continued – The List of Practical Solutions
6. Elephant in the Test Room #1 Continued – The ‘Get Around’ Explained
7. Elephant in the Test Room #1 Continued – The Solid State Approach
8. Elephant in the Test Room #1 Continued – The Final Piece in the Conventional Approach
9. Elephant in the Test Room #1 Continued – Linearization of EMC Amplifiers
10.The Linearization of EMC Amplifiers Continued and Introduction to Elephant in the Test Room #2
11. Training the Intern and Elephant in the Test Room #2 Continued
12. Elephant in the Test Room #2 Continued and the Design Guide Article