Ron Brewer
EMC/ESD Consultant
Shielding has been with us a long long time. Early AM radios had shielded RF and IF transformers, shielded electron tubes, and compartmentalized shielded chassis. These shields were necessary to prevent RF pickup, feedback, and oscillation by the electron tubes, radiation from the local oscillator, RF contamination of the IF strip, and crosstalk within circuit wiring. By the mid 1940’s there were a number of military RFI specifications to be met and RF gaskets were in use (beryllium copper, silver elastomers, and monel wire mesh). In 1956 a tri-service shielded enclosure measurement specification was released called MIL-STD-285. Fifty years later it is still being used to evaluate shielded enclosures. This standard has been used to measure almost every kind of shielded enclosure, but it was originally designed to measure the enclosure attenuation provided for sources located outside the enclosure. It makes a difference how the enclosure is measured. The measurement should match the way the enclosure is used.
The same thing is true of enclosure design. The design should first consider the problem. Are we dealing with Radiated Emission, Radiated Susceptibility, Inductive and/or Capacitive Crosstalk, or some combination thereof. We also need to consider whether the problem is plane wave, electric, or magnetic field coupling. It doesn’t make since to worry about providing 120 dB of EF attenuation when the equipment we’re trying to protect is only sensitive to or only produces HF’s. Because shielded enclosures are designed to contain and/or exclude electromagnetic energy it is necessary to discuss some of the characteristics of radiated electromagnetic fields and waves in order to understand the design process.
Fields and Waves
A stationary charge may cause upset to an electronic device by exerting a repulsive force on like charges in the device (this is especially true with semiconductors), but if the electrostatic charge is not changing, it does not create an electromagnetic field. On the other hand current is charge in motion, and current creates a magnetic field. If the current is steady state (DC), the magnetic field will be constant. A constant magnetic field does not create a radiated electromagnetic field. However when charge is accelerated (decelerated) current increases (decreases) creating a changing magnetic field which in turn creates a changing electric field, etc. and electromagnetic energy is radiated away from the source. The energy can be developed from either a high impedance (High voltage – low current) electric field source or a low impedance (High current – low voltage) magnetic field source. Monopole and loop antennas are good examples of these two sources. This is illustrated in Figure 1.

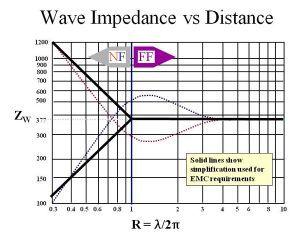
Near to the source, the relationship between the electric and magnetic fields is very complex and although both will exist, the field characteristic can be primarily electric or magnetic. Farther from the source the relationship between the electric and magnetic fields becomes constant with ratio of E/H = 120 π. This is illustrated in Figure 2. The simplifications and approximate distance for the change from near field to far field used by the EMC folk is R = λ / 2π. This makes an assumption that the dimensions of the source structure is less than ½ wavelength. Antenna designers who strive to be more precise may get upset by this!
Shielding Effectiveness Models
There are three models typically used to describe shielding effectiveness. One of these works only at the low frequencies (including DC). The other two are usable for RF. At the lower frequencies where the inductive reactance of the material is less than the materials resistance, shielding effectiveness is primarily determined by the materials conductivity (for EF) and permeability (for HF). This often leads to the erroneous belief that the materials resistance determines its shielding effectiveness. Various RF gasket manufacturers have attempted to use materials volume resistivity to define shielding effectiveness and then apply these values over frequency ranges where the values are invalid. If one considers the behavior of a capacitor from DC throughout a wide frequency range, it’s obvious that a structure can have extremely high resistance at DC and very low RF impedance at the higher frequencies. The reverse is true for inductance! A reflective shield requires both low resistance and low RF impedance. RF impedance cannot be determined by only measuring the resistance.
Circuit Approach
In the midrange of frequencies from roughly 300 kHz to 3 GHz, shielding effectiveness can be modeled using the circuit approach. In this frequency range shielding can be determined from the materials transfer impedance. This approach was developed by Wheeler in the mid 1950’s to estimate magnetic field shielding of an enclosure. The technique has been expanded to include magnetic, electric, and plane wave shielding. The circuit approach describes a shielded enclosure as either a short circuited loop antenna for magnetic fields or a fat electric dipole antenna for electric and plane wave fields. Modeling the enclosure as an antenna permits the circuit approach to provide answers that consider the overall size of the enclosure as well as the shielding material characteristics. The method essentially determines the RF current that can be induced into the skin of the enclosure (as an antenna structure of a given size) and what electromagnetic field levels will be developed within the interior of the enclosure by the induced currents being coupled through the transfer impedance. This method would be easier to adapt for the analysis of apertures or discontinuities than the transmission line approach described next, but it still has its shortcomings. When the dimensions of the enclosure (with respect to frequency) permits the development of standing waves, i.e. the longest dimension is equal to a half wavelength, then the enclosure becomes an RF cavity and the transmission line approach becomes a good model to use.
Transmission Line Approach
The transmission line approach was developed by Schelkunoff in the early 1940’s. Briefly, the difference in the radiated field and shield impedances results in some of the RF energy incident on the enclosure surface being reflected (R) from the surface, and some energy being absorbed (A) as it travels through the shield material. As such, shielding effectiveness can be described in terms of the individual contributing factors that represent the change in field strength. This approach is easy to visualize and it is frequently used in presentations describing the theory of shielding.
Schelkunoff’s method is particularly well suited for large homogeneous enclosures without discontinuities where the wavelength is longer than the dimensions of the enclosure. The method does not account for the size of the enclosure and because a plane wave assumption is being made, it does not provide accurate estimates of magnetic or electric field attenuations at low frequencies where dimensions of the enclosure are small with respect to the wavelength. Schelkunoff’s approach was modified by Richard Schultz (the author of MIL-STD-285) and the combined Schelkunoff-Schultz analysis method, although much improved, still has difficulty estimating the magnetic field attenuation. The most accurate analysis approach for magnetic field shielding was developed by King in 1933 and is based upon Maxwell’s equations. A lot of work was done by John Quine et. al. at RADC, using the transmission line approach to analyze shielded enclosure discontinuities such as apertures and RF gasket materials. Although there will be elements of each of these approaches scattered throughout this article, the discussion will primarily focus on the transmission line approach. Some pedagogical simplifications will be made, which may annoy some readers, but it will make it easier to understand.

There are two cases to examine. Case 1 where the RF source is located outside the enclosure and Case 2 where the RF source is inside the enclosure. Refer to Figure 3 for an illustration of these two cases.
In both cases,
SEdB = 10 log (P1/P2) = 20 log (F1/F2 )
Where F1 and F2 are the magnetic, electric, or plane wave field intensities at the enclosure surface closest to the RF source and on the opposite side of the enclosure wall respectively.
For Case 1, where the source is external, the overall shielding effectiveness (in dB) can be generalized and approximated by:
SEdB = AdB + R( )dB + BdB
Where:
A = Absorption loss in dB
R( ) = Reflection loss (Not really a loss but rather a redirection of the RF energy. Because the RF source is located outside the enclosure the redirected energy can be viewed as a loss)
B = Correction for multiple internal reflections. Typically only significant for very thin materials when the absorption loss is less than 10 dB. It will not be discussed in this article.
At the higher frequencies, an enclosures shielding effectiveness is dominated by absorption which is independent of the type of wave illuminating the enclosure and is given by the following expression:
AdB = k t (μ σ FMHz)0.5
Where:
k = 3.34 (if t is in mils) , k = 0.131 (if t is in mm)
t = thickness of the material in mils or mm (this will determine which k to use)
μ = relative magnetic permeability
σ = relative conductivity
FMHz = Frequency in MHz
The RF energy reflected from the enclosure surface results from the mismatch between the incident wave impedance (Zw) and the shield material impedance (Zs). For distant sources where the separation distance (d) is equal to or greater than d = λ / 2π or about 1/6 wavelength (plane wave region) the wave impedance is constant at Zo = 120 π ohms regardless of the originating source impedance or separation distance. For nearby sources on the other hand, the wave impedance Zw varies with both the source impedance and the distance from the source to the shield material. The wave impedance of low impedance sources (magnetic field) will be less than 120 π (i.e. 377) ohms and will increase to that limiting value as distance increases. The wave impedance of high impedance sources (electric field) will be greater than 120 π ohms and will decrease to that limiting value as distance increases. As a result, there are 3 equations that are used to calculate the reflection from the shield surface. These equations assume that the ratio of Zw/Zs or Zs/Zw >10. When λ / 2 π r or 2 π r / λ = 1 the EF and HF equations become equal to the plane wave equation.

Plane Wave: RdBP = 20 log (120 π / 4 Zs )
Electric Field: RdBE = 20 log [(120 π / 4 Zs )( λ / 2 π r)]
Magnetic Field: RdBH = 20 log [(120 π / 4 Zs )( 2 π r / λ )]
Where:
Zs = 3.68 * 107 (μ FHz / σ)0.5
μ = relative magnetic permeability
σ = relative conductivity
FHz = Frequency in Hz
Note that Zs increases with increasing frequency which results in a decreasing value for reflection. Figure 4 illustrates and compares the shielding effectiveness of copper and iron.
For Case 2, the overall shielding effectiveness (in dB) is approximately:
SEdB ≈ AdB
Where:
A = Absorption loss in dB
R( ) ≈ 0 dB
The reason that reflection R( ), was not considered a loss in this case is that the energy that is reflected/redirected from the interior wall is still in the enclosure. Admittedly, it is not zero but its effect can still be quiet small. These internal reflections within the enclosure may result in evanescent waves that are out of phase with the original signals that created the interference and either interfere with the operation of the circuits that produced them or combine with normal waves resulting in an increase in EF levels. Even if that does not happen, the reflected waves can exit through apertures simultaneously with normal incident waves and result in an increase in the overall field strength. As the enclosure size increases to the point where standing waves can exist, resonant amplification can occur. When this occurs EF levels within the enclosures can typically increase by 30 to 40 dB, dwarfing the previous problem.
Even so if we have a good enclosure it really doesn’t matter. For example, most sheet metal military avionics enclosures are made from 30 to 40 mil aluminum.
AdB = 3.34 * 30 ( 1 * 0.64 * 100) 0.5 = 802 dB attenuation at 100 MHz
We can’t measure that much attenuation and we are not likely to be able to achieve it either but it’s evident that not adding in the reflection didn’t matter.
Enclosure Size
The fact that the size of a shielded enclosure has an effect on its shielding effectiveness is not often discussed. It does this primarily from the perspective that the enclosure Q is proportional to the energy stored in the cavity volume to the energy dissipated in the internal surface area. The shielding effectiveness is directly proportional to the enclosure volume and inversely proportional to the Q which is altered by any lossy elements such as RF gaskets, seams, dissimilar materials, installed components, etc. For those readers that are interested in more information about this topic, a significant amount of research (with papers) has been done in this area by John Quine, et. al. at RADC, Rome, NY.
In addition, the size determines enclosure resonance frequencies. The resonances makes the SE fluctuate as a function of frequency. The attenuation may remain constant but the field strength internal to the enclosure increases at the resonant frequencies and the higher internal field strength values make it appear as if the SE of the enclosure has deteriorated. Typical equivalent loss in SE resulting from resonance is 30 to 40 dB. However, studies done at Georgia Tech have indicated as much as 60 dB for very high Q enclosures.
For a simple rectangular enclosure (dimensions L, W, H in meters) the various resonant frequencies can be calculated from the following expression:
TElmn = 0.5 C [(l/L)2 + (m/W)2 + (n/H)2]0.5
Where L< W < H and l, m, and n are integers.
Setting l and m = 1 and n = 0 permits us to calculateTE110, the lowest resonant frequency for the cavity.
The increase in field strength is dramatic! Based on studies done on resonant cavities for reverberation chamber tests for MIL-STD-461 testing by USN Dahlgren, VA, [M. Hatfield, et al] the average EF strength inside an unloaded (empty) reflecting cavity can be calculated by:
E(V/m)ave = [(Q Pin ηant Zo Co) / (12 π Vvol FMHz)]0.5
Note: The peak field strength 6 to 8 dB greater than the mean and the field distribution levels throughout the enclosure are not uniform. Since cavity Q’s are proportional to the energy stored in the volume of the cavity to the energy dissipated in the impedance of its internal surface area (Vol/As), for the same cavity configuration, using materials with the same magnetic permeability (i..e. 1), the Q’s would be proportional to the ratios of the surface conductivity of the cavities. For some idea of the Q values, at 2000MHz an empty copper enclosure would have an unloaded Q of about 26,000, and a loaded Q of about 2,600. Here’s the effect of generating a 2000 MHz 10 watt signal inside the enclosure. The antenna efficiency is assumed to be 0.9:
E(V/m)ave = [(Q Pin ηant ZO CO)/(12 π Vvol F)]0.5
Becomes:
E(V/m)ave = [(2600 * 10 * 0.9 * 120 π * 300) / (12 π * 1 * 2000)]0.5
= 187 V/mave and 374 V/mpeak
This can be a major problem, particularly for designers and builders of spacecraft.
In general, loading the enclosure with conductive or absorbing materials reduces the volume and increases the internal surface area. Baffles and compartmentalization pushes resonant frequencies higher, reduces Q, and provides localized shielding of components/modules.
These high level calculated shielding effectiveness values indicate best-case shielding effectiveness since they do not include the effects of apertures or other discontinuities. Unfortunately, it is not practical to build an all-welded enclosure. Most enclosures require various openings for controls, access panels, ventilation, viewing, etc. These aperture/discontinuities account for most of the leakage in a shielding enclosure
Aperture Effects
Apertures come in different shapes, but considering the shielding effectiveness as the inverse of the radiation efficiency of an equivalent shaped slot antenna provides a simple model for calculating aperture worst‑case shielding effectiveness. Some error results from this assumption, but it is adequate for design because the shielding effectiveness is greater than the calculation indicates. Shielding effectiveness of a single aperture with the largest opening dimension (D) is given by the first part of the following equation. The second part of the equation corrects for multiple equal sized (D) apertures.
SEdB = 20 log l/2 D ‑ 20 log n | S≤ λ/2
Where:
k = 20 for slot and k = 40 for a round hole
D = length of slot (meters) and L > w and L >> t or Diameter of Hole (meters) D >> t
λ = wavelength in meters
n = number of apertures within λ /2
This equation can be solved in terms of dimension (D) to determine what size aperture is required for a given attenuation, but in general, apertures should not be longer than D = l/50. This makes for a very small opening! For example, to achieve acceptable attenuation values at a frequency of 10 GHz – the 10th harmonic of a 1000 MHz clock (not unusual for high-speed digital devices), apertures should not exceed 0.6 mm. In a manufacturing environment this means continuous seams.
Aperture Sealing
Notwithstanding the type of shielding panel or skin material used, the enclosure shielding effectiveness depends upon how well the panel or skin is sealed into the enclosure, i.e., the quality of the RF bond across the seam aperture. Any isolated panel/skin that is not adequately grounded/bonded to the enclosure can behave as an antenna structure. Grounding the panel at only one point will reduce its antenna efficiency and often prevent it from acting as an antenna, but it will not eliminate leakage through the rest of the seam.
The best methods for sealing the perimeters of shielded apertures, in order of effectiveness, are welding, brazing, soldering, and riveting, except in a high shock and vibration environment where riveting is better than soldering. Unfortunately, these methods prevent easy access for maintenance and repairs. Installing closely spaced screws or clamps permits, but does not facilitate, field removal. Therefore, enclosures generally use positive contact designs to provide and maintain a low RF impedance connection across mating surfaces. This may take the form of bosses, segmented or interlocking seam edges, overlapping surfaces, or RF gaskets. Depending on the seam design these approaches may eliminate the need for fasteners altogether but in any case will permit the fasteners to be spaced farther apart.
There are over 2000 different RF gasket designs available based on combinations of materials and construction. With good printed circuit board design, a minimum of 60dB is adequate for most commercial applications. Military equipments will typically require 80 to 100 dB. The various RF gasketing materials have substantial differences in their electrical, mechanical, and corrosion properties. Plus, each is better suited for some applications than others. The choice depends on the type of enclosure seam in which the gasket is used. Just based on attenuation, for levels greater than 80 dB, beryllium copper, tin, and silver plated metal or metal filled elastomer gaskets are the most popular. From 60 to 80 dB add in monel, nickel, SnCuFe, and silver plated fabric. For 60 and below every material can be used.
Seam Configurations

There are four seam configurations to choose from. These are (1) the isolated seam, (2) the compression seam, (3) the shear or wiping seam and (4) the insulated or choke seam. These seam configurations are illustrated in Figure 5. The isolated seam can best be described as a butt joint. An example is the top and bottom seams between blank panels or pull-out drawers mounted in a rack. Because there is no overlap it is difficult to use conventional gasket materials, and the preferred sealing method is conductive foil or cloth tape placed over the seam. This static (fixed) configuration is used frequently in lightweight spacecraft and satellite applications, but it’s meant to be a permanent solution that will not be repeatedly opened and closed.
The compression seam tends to be the most frequently used type of seam. It may not be the best but it works. This configuration is also intended to be a static joint. In this application, panels overlap the perimeter of the apertures. If the contact surfaces are conductive these can generally meet the 60 dB commercial requirement with the use of closely screws, especially hi torque types. For higher levels of attenuation this seam design can also be sealed with any type of RF gasket material. Since the gasket material compression forces are normal to the panel, uniformly spaced threaded fasteners or clamps still must be used around the perimeter to maintain the RF seal. Choosing a lower compression force gasket enables the use of lighter weight enclosure materials and wider spacing of the fasteners. As enclosure configurations become smaller and more complex gasket choices become limited, form-in-place and printed or vulcanized elastomer gaskets are used.
The shear seam is the only dynamic configuration, and must be treated differently than the other two. This type of joint is constructed in several different configurations, i.e., pan-edge, knife-edge, modified knife-edge, and/or longitudinal. These designs align the mechanical forces parallel to the panel surface so no fasteners or clamps are required to preserve the shielding. Thus this design can eliminate the need for fasteners. Plain pan covers can be used but without bosses or segmented edges it is difficult to assure good contact around the perimeter. If RF gaskets are required for higher attenuation, metal-finger gaskets are normally used for this application, however some fabric-over-foam configurations have been used. If fabric gaskets are used care should be taken to assure that the seam design does not abrade the fabric. This configuration has the highest shielding effectiveness over the widest frequency range, plus it is self-cleaning. Because of the difficulty of retrofitting this configuration into an existing product, this design should be considered from the beginning of the project. When designed in from the beginning it typically has the highest performance with the lowest overall cost.
The insulated (choke) seam is quite different from the previous three seams. Those seams are broadband RF configurations, which rely on making a low impedance metal to metal RF bond across the mating surfaces. The choke seam is for those high frequency equipment designs that do not need a broadband solution. Some designs even require that the cover must be insulated from the base. Some even require that the metal cover be covered with plastic to minimize corrosion and make it easy to clean. So long as the attenuation is required only in a high but narrow frequency range this can be accomplished with a microwave choke seam. This seam is an RF filter. Each side of the seam has a machined λ/4 or a λ/2 groove which reflects an out of phase signal component to combine with and attenuate the signal. The groove can be stagger tuned using a stepped configuration to increase the bandwidth, but unfortunately cannot achieve the bandwidths of the previous three designs.
Shielding Design Process
This approach doesn’t always work but it provides a methodology to get started.
Start by defining the EUT’s radiated requirements. This can be done by measuring the ElectroMagnetic Environment (EME) or by referring to the current military or commercial requirements that apply to the equipment being shielded. Once that’s done, determine the EUT radiated emission and susceptibility levels. This can be done by measurement or by prediction and analysis (P&A). There are three frequency ranges of interest: (1) less than 100 kHz, (2) between 100 kHz and 100 MHz, and (3) greater than 100 MHz.
These levels are then compared with each other and to the defined environmental requirements to determine worst case shielding effectiveness needed. Note: It doesn’t happen often but sometimes the radiated emission levels exceed the radiated susceptibility levels. This is indicative of a potential major self-compatibility problem and must be handled separately from environmental EMC.
To account for variations in the electromagnetic characteristics from one system to the next an EMC Safety Margin (EMCSM) is added. The EMCSM is 6 dB if the levels were measured and 12 dB for P&A.
Frequencies less than 100 kHz.
Emission or susceptibility frequencies less than 100 kHz implies a magnetic field (HF) coupling problem. In this case the shielding effectiveness is highly dependent on the type of material used for the enclosure. Regardless, it is necessary to start by determining the shielding effectiveness (SE) required at the highest frequency and then add in the appropriate EMCSM.
Next, assume a low-cost permeable material and calculate the thickness (t) required to produce an absorption loss (A) = SE + EMCSM. Stop if the calculated thickness (t) is less than the maximum design thickness otherwise increase the thickness and/or change to a higher permeable material and repeat the calculation. Cold rolled steel is a good start followed by hot rolled steel and then purified iron. When the required thickness-permeability forces a selection of exotic high permeable materials such as mu metal, conetic, supermalloy, reconsider thickness constraints before making a decision to use these materials.
For HF shielding, overlapping seams (with minimum air-gap) are required for flux transition across the seam. Overlap requirements are 10 to 100x the thickness of the material but 0.5 inch is typically used. RF gaskets are not used. Do not use butt joints.
Frequencies over 100 kHz
Emission or susceptibility frequencies that are over 100 kHz can be either HF or EF coupling problem. In either case at these higher frequencies, conductive materials can be used. The design approach is determined by whether the RF source is inside or outside the shield, how much attenuation is needed, i.e. greater or less than 60 dB, and whether the frequency is greater or less than 100 MHz. Start by calculating the shielding effectiveness (SE) required at the highest frequency and add in the appropriate EMCSM.
If the source is inside, assume a low-cost conductive material (such as aluminum) and calculate the thickness (t) required to produce an absorption loss (A) = SE + EMCSM. Stop if the calculated thickness (t) is less than the maximum design thickness otherwise increase the thickness and/or change to a permeable material and repeat the calculation. Cold rolled steel is a good start followed by hot rolled steel and then purified iron.
If the source is outside, assume a low-cost conductive material (such as aluminum) and calculate the reflection from the shielding material first. In this case the reflection (R) requires about one skin depth making it essentially independent of the thickness of the material. Especially at the higher frequencies. If the reflection is adequate at the lower frequencies then the material selection is complete. If not then calculate a thickness (t) required to produce an absorption loss (A) such that A + R = SE + EMCSM. Stop if the calculated thickness (t) is less than the maximum design thickness otherwise increase the thickness and/or change to a permeable material and repeat the calculation.
Once the material characteristics are established, seam design and RF gasket choices are made. This is based on attenuation vs. frequency and summarized in Table 1.
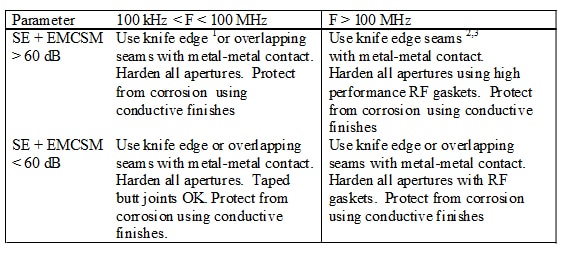
Note:
1. Simple knife edge/pan contacts can be dimples or bosses
2. If new construction knife edge/pan type construction is preferred
3. If existing hardware, use a high performance continuous seal
ABOUT THE AUTHOR
Ron Brewer is currently a senior EMC/RF engineering analyst for NASA/Analex at the Kennedy Space Center. The NARTE certified EMC/ESD engineer has worked full time in the EMC field for more than 30 years. Mr. Brewer was named Distinguished Lecturer by the IEEE EMC Society. He has taught more than 385 EMC technical short courses in 29 countries and published numerous papers on EMC/ESD and shielding design. He completed undergraduate and graduate work in engineering science and physics at the University of Michigan. Email: ronbrewer@ieee.org.
