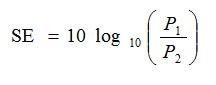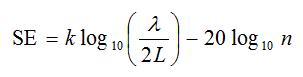Brian She
Laird Technologies
ABSTRACT
There is a growing need to evaluate the shielding effectiveness (SE) of board level shielding (BLS). By means of a reverberation chamber, we performed a series of shielding effectiveness test for board level shielding products with different apertures. In addition, an analytical SE formulation has been developed in comparison with the SE measurement result.
Key words: Apertures, Shielding effectiveness, Board level shielding, SE calculation
INTRODUCTION
In the electromagnetic shielding practice, board level shielding is widely used for isolating electromagnetic interference, especially on the circuit board with intentional RF emission. A perfect BLS will have no apertures and fully be soldered on the ground plane of the board all around its perimeter, so that it can reach the maximum shielding effectiveness. However, we need to make the BLS lighter weight, more convenient manufacturability, and we also have to avoid cavity resonance inside the BLS, dissipate the heat and let microstrip trace to go through, so there should be several apertures opened on the BLS, to evaluate the effect of apertures on shielding effectiveness, we performed several kinds of test on different apertures for comparison, and we also run some calculation tools to plot the corresponding SE data based on shielding theory.
Shielding Theory of Material with Apertures
Shielding Effectiveness (SE) measurement of materials is a comparable method to evaluate the shielding performance, the current universal method used for obtaining a value for the SE is to measure difference between the received power with and without the shielding parts assembled, the equation expressed in dB is:
P1 =the received power without shielding;
P2 = received power with shielding;
The shielding effectiveness of an aperture, and ultimately of the enclosure itself, is a function of its size, shape and number of apertures .The worst-case shielding effectiveness of the slot (L) based on the radiation efficiency of a slot antenna, provides a simple model for calculating the worst-case shielding effectiveness of an aperture. A different value of constant (k) is for a slot (20) or for a round hole (40). A slot can be considered to have a length-to-width ration of 4:1 or greater. For geometrically even holes such as squares or hexagons, 40 may be used as the constant.
Shielding effectiveness of a single aperture with the largest dimension of the opening length (L) is given by:
λ = wavelength
k = 20 for a slot or 40 for a round hole
L = largest dimension of the aperture which is ≤ λ/2
For more than one aperture, the SE must be subtracted by 20 log10 of the total numbers of apertures within a half wavelength, so updated equation is:
n = numbers of apertures within a half wavelength
Theoretically, Apertures placed more than half a wavelength apart do not in general worsen the SE value, but half a wavelength at most concerned frequencies is usually big enough for the actual spacing between apertures on board level shield.
This equation is based on slot antennas under free space plane-wave propagation i.e. far-field conditions when the wave impedance in air is (120p) Ohms, while for many cases in real practice, the BLS is located in near-field of the source at certain frequencies, and the SE may be worsen in this condition, so we should state here that one should consider the distance from the aperture to the radiation source when using this SE calculation formula.
SE Calculation for Apertures
Based on the before-mentioned equations, we developed a modeling program (Microsoft Excel format) for the calculation of shielding effectiveness resulting from apertures (holes and/or slots) in printed circuit board shields or other enclosures, The program provides an estimate of the resultant shielding effectiveness due to ventilation holes needed for heat management or folded metal that form slots on the sides of a board level shield.
In the shielding effectiveness input box, several input options should be selected, the main input section is the maximum dimension of the aperture, which will determine most of the level of SE, to elaborate the apertures, we also need to decide the following items:
A, whether the emitter is inside or outside of the shield: the SE calculation formulas are different under these two conditions because the reflection portion needn’t be considered if the emitter is outside.
B, the spacing between apertures: the numbers of apertures within a half wavelength N will be figured out by this input.
C, correction factors such as the shielding material (permeability and conductivity) and the aperture shape (it is more round or more slot-like.).
SE Measurement in a Reverberation Chamber
A Radiated Shielding Effectiveness testing was performed in a reverberation chamber. The chamber has metallic, highly electrically reflective walls, which, in conjunction with a mode stirring paddle to produce statistically uniform internal electromagnetic fields. The mode stirrer was installed in the room with transmitting antenna, and the receiving antenna was placed in another shielding room, the test sample was mounted on a shielding wall to separate the two antennas. An overview of this test set-up is shown in Figure 2.
The above setup diagram just describes the main structure of the test, to achieve sufficient dynamic range, we also adopted power amplifier in the circuit loop, as well as the low noise preamplifiers.
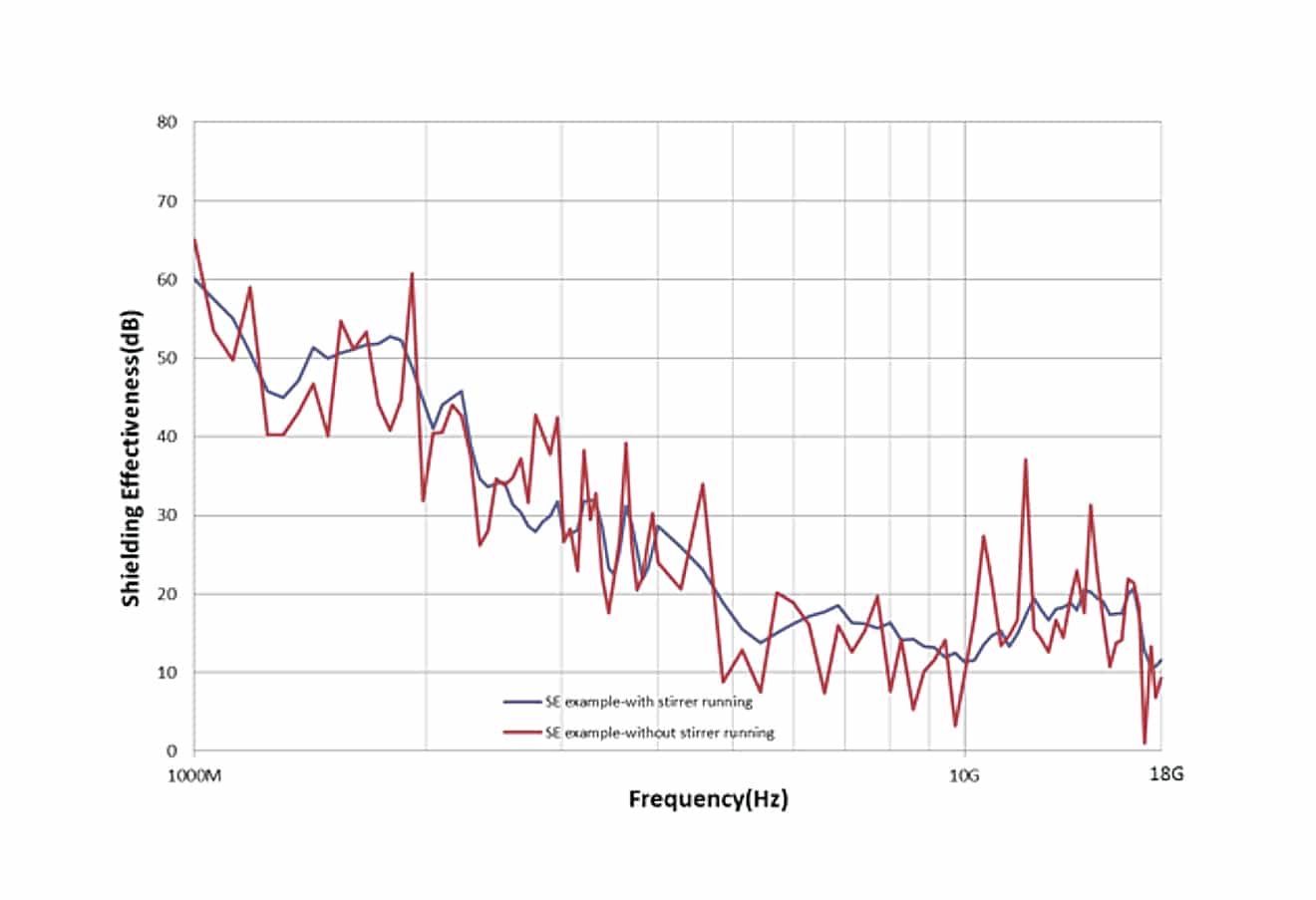
For the SE test in a reverberation chamber, we need to run the mode stirrer to create a uniform EM environment in the transmitting room, in such condition, the time-averaged fields (or power density) inside such a chamber are approximately equal in amplitude. To evaluate the performance of the mode stirring system, we tested SE with and without the stirrer running, Figure 3 is an SE example for BLS testing, it shows that the data curve is more fluctuated when testing without stirrer running.
The test sample is made of copper sheets as it is very conductive and it is easy to cut into different apertures. After the test sample is done, we mount it onto the test fixture by four aluminum clamps, and we also put conductive foam between the contact surfaces for better shielding. The antenna should be placed far enough so that the EM wave at the surface of the object is stable plane wave, here we placed the transmitting antenna pointed at the center of the paddle, which is about 1.5m away from the test sample. In the other enclosure, the receiving antenna was pointed directly at the test sample 50cm away, so that the most received energy is from the BLS aperture. The test frequency starts from 1GHz to 18GHz, thus, we can get the test data which is quite stable and repeatable. Figure 4 and Figure 5 shows the SE test set-up in the reverberation chamber.


Discussion of the SE Result
To obtain relatively comparable test results, we built some specified dimensions of the test samples, including holes and slots. The following are some examples for SE comparison.
1, SE comparison between different dimensions of holes (Figure 6).
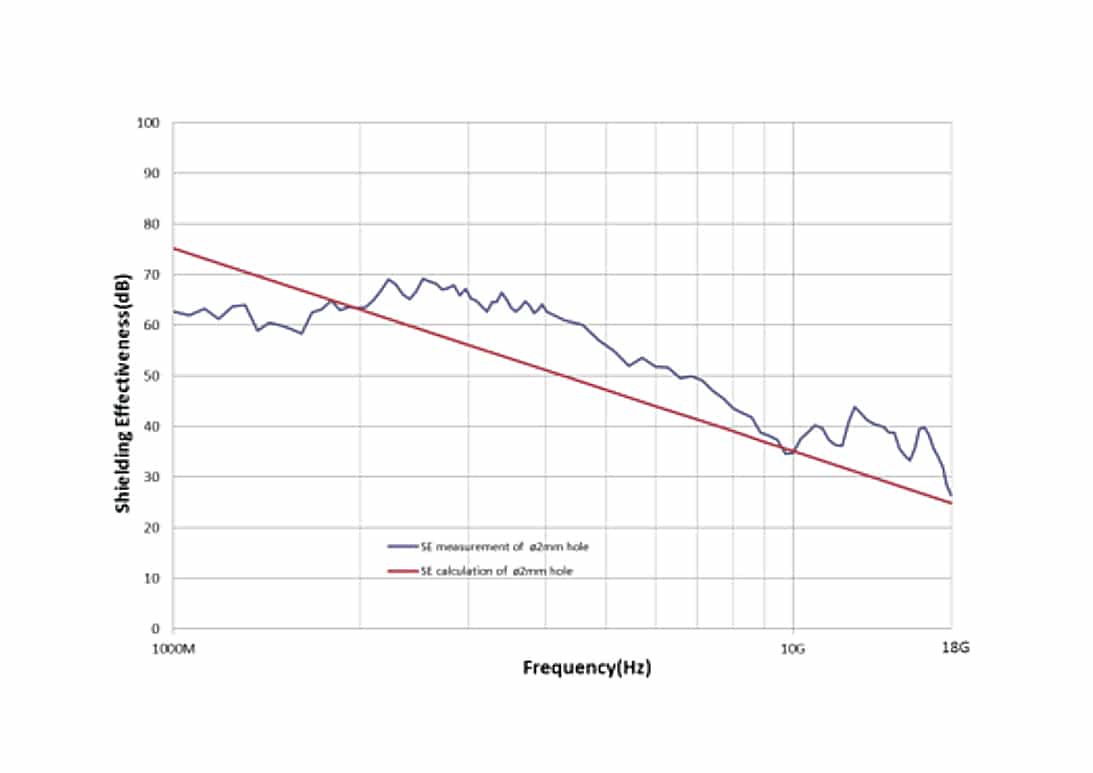
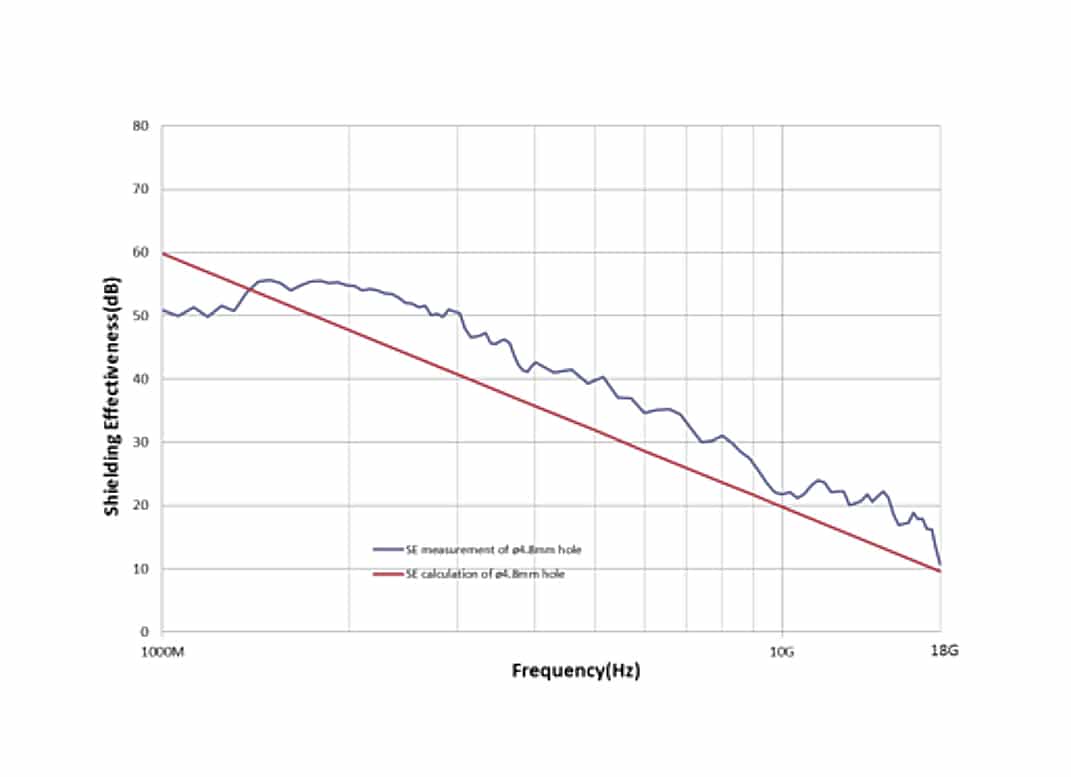
The SE results by both measurement and calculation are shown as below, Figure 7 to Figure 9 are the SE data of different sizes of round holes. First, as to the comparison of ø2mm, ø4.8mm and ø11.2mm holes, the SE between measurement and calculation are matched, although not very well, we can see that they have the same tendency, but in most frequencies, the calculated SE value is lower than the measured SE value, this is reasonable because the calculated SE always represents the worst case. If we look at the details of each figure, the measured SE at low frequencies is not as high as expected by calculation, the most possible reason for this mismatch is the methodologies difference between measurement and calculation, for SE calculation, the reference level is derived from an infinite large opening, while in real test, we use a specified opening to get the reference level, thus there are reflections should be considered in SE measurement.
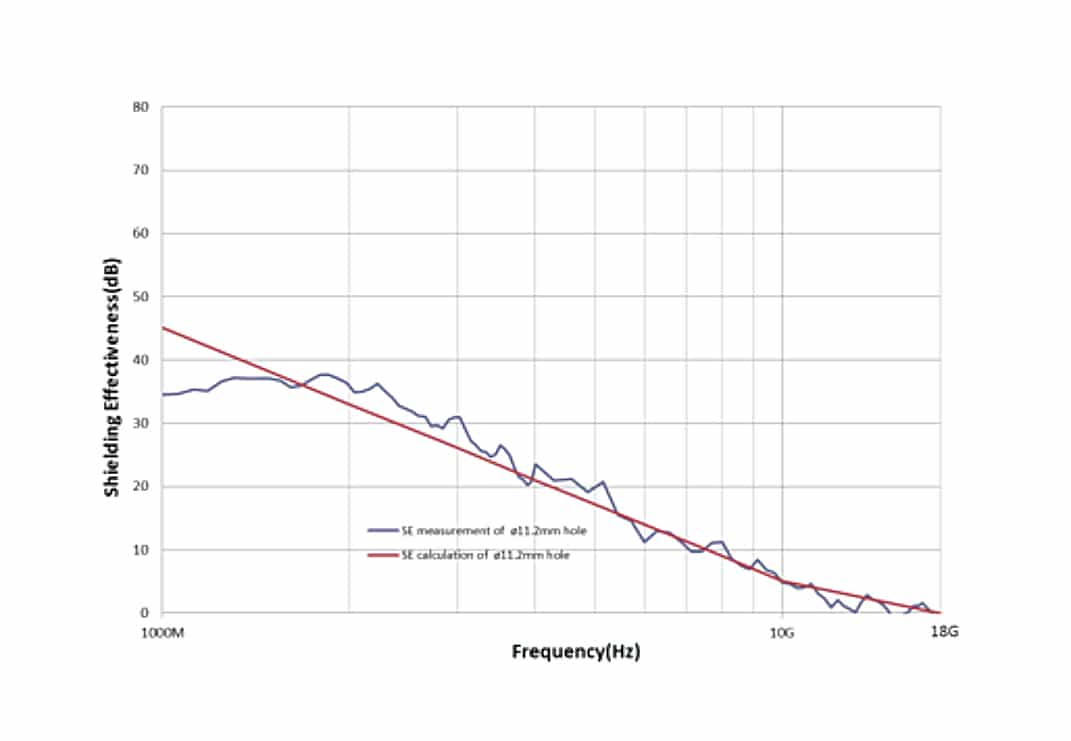
2, SE comparison between diff erent hole numbers (Figure 10).
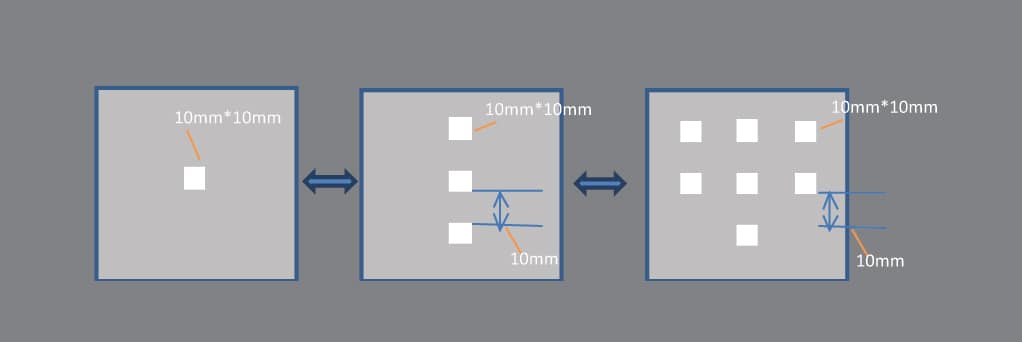
In real application, we usually use the BLS with several hole on it, so it is worthy to study how much effect of the numbers of apertures contribute on SE, figure 11, 12 and 13 are the SE of apertures with one hole, three holes in line and nine holes in matrix, each of the hole is 10mm*10mm in square shape.
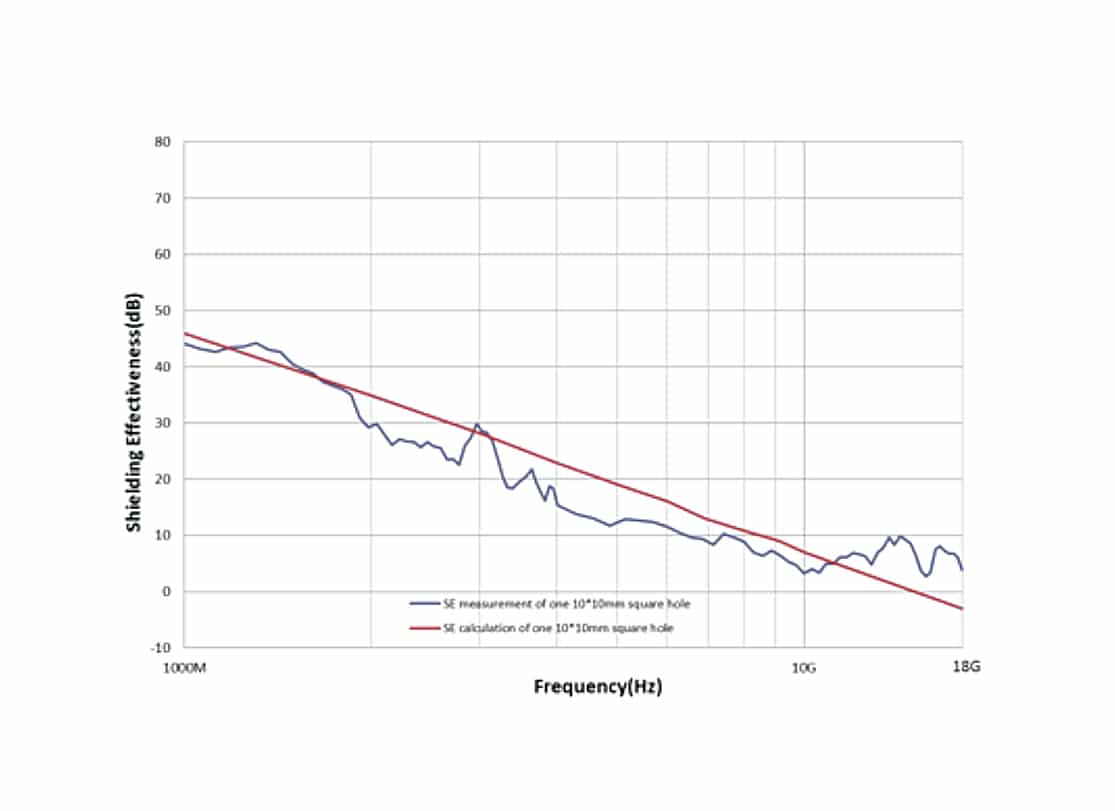
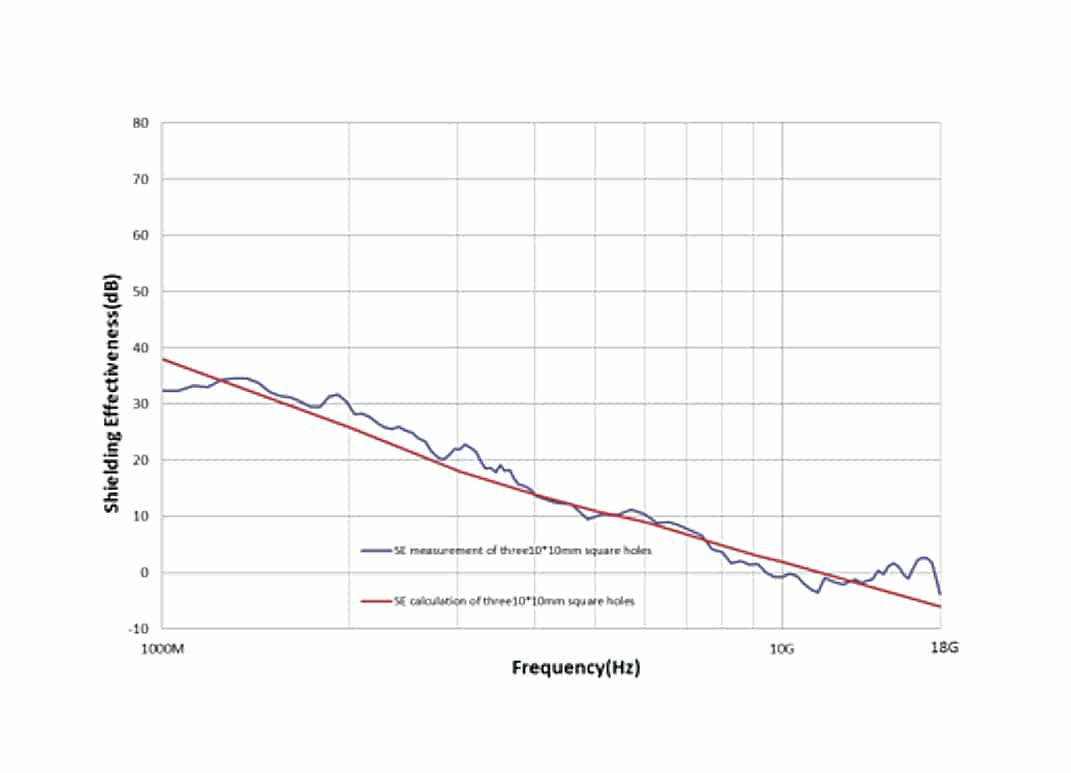

Let’s compare the SE differences between one hole, three holes and nine holes, firstly, there is about 10dB difference between them in lower frequency range, both in measurement and calculation. however, in higher frequencies(above 10GHz), the calculated SE values almost stay in the same level between this three, and the measured SE gaps also narrowed to about 5dB, so we see the whole SE curve become more flat when the hole number increases. According to the calculation formula, this is reasonable because the calculation factor “n” (which means the number of apertures with λ/2) will minimize to “1” as the frequency goes higher, thus, it implies that in higher frequencies, the apertures outside the “λ/2” circle area won’t make effect on the SE value, Figure 14 is the Aperture Depiction, Showing Circles with Diameter of λ/2.
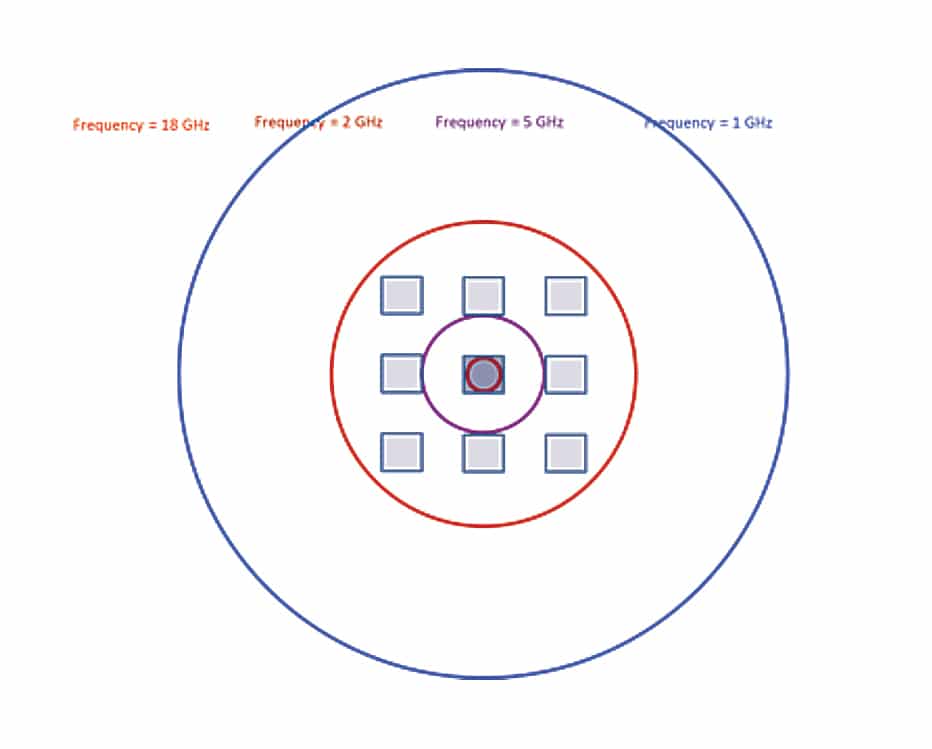
We see that SE could even go to negative in the foregoing example, It should be clear that an inefficient radiation source (e.g. an electrically small circuit) can become many orders of magnitude more efficient by coupling to a larger conducting structure. Therefore it is not only possible, but common, for a shielding enclosure with apertures to increase the radiated emissions due to the sources enclosed. In other words, the SE of a shielded enclosure can easily be less than 0 dB (i.e. the enclosure amplifies the radiation) at some frequencies. Therefore, it is not safe to assume that some shielding is better than no shielding.
3, SE comparison between holes in line and slot (figure 15).
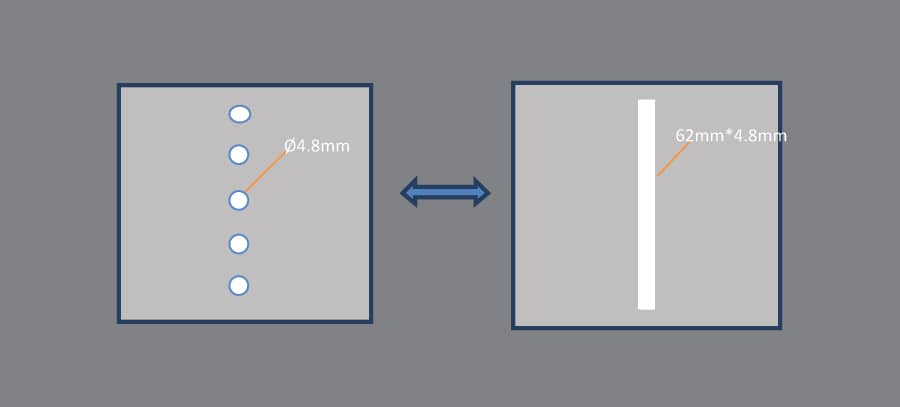
In order to improve the shielding performance, we should study on SE of different type of apertures, the typical research is comparison of holes and slots, of which the SE data are shown in figure 16 and 17, the five ø4.8mm holes in line versus one 62mm*4.8mm slot, we compare them because they occupied similar area of the BLS, and we can see that there is big difference of SE between them (the SE of slot is about 40dB lower than the SE of holes), Please note that the polarized direction of incident wave is parallel to the long side of slot, so the test data is quite coincident with calculation. In design for EMC, it is important to divide a big aperture into several small one when design the BLS, and of course the round holes always perform the best SE compared to other apertures.
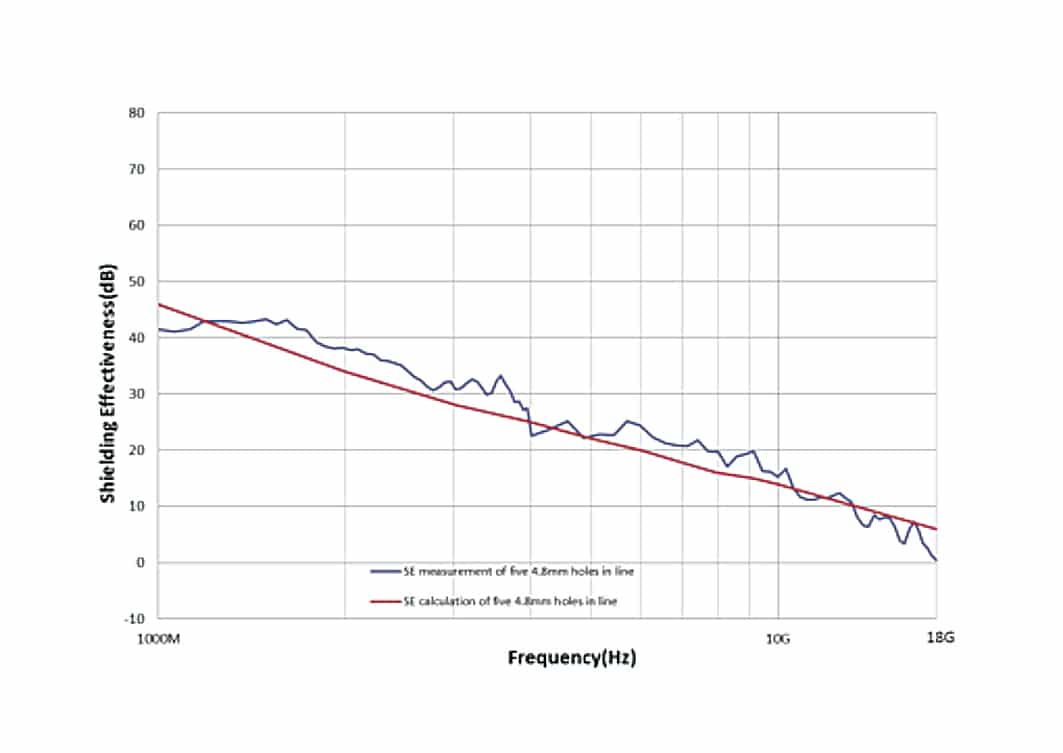
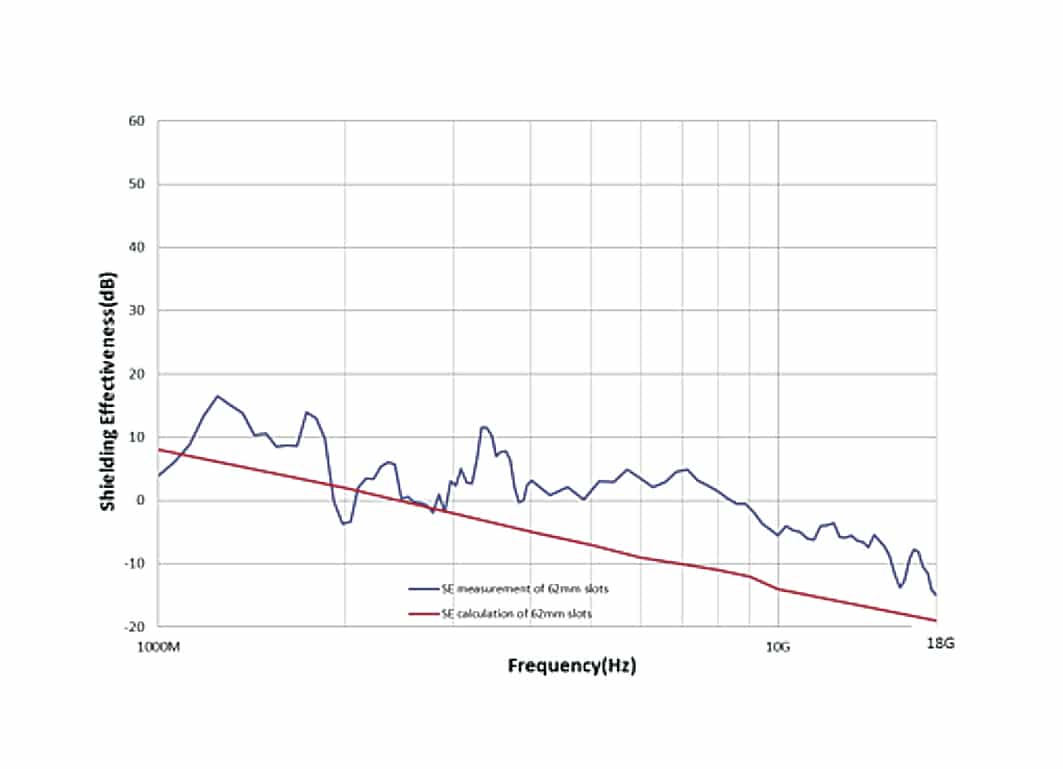
From all the SE data line above, we can say that generally, the SE data from calculation is in agreement with the measurement, although there are mismatch points at some frequencies. We know that SE test result may be influenced by many factors, such as chamber resonance, test set-ups, cable coupling etc., so it is meaningful to do comparison in different test labs by different test methods. In terms of the SE calculation formula, the biggest disadvantage is it is helpless for complex apertures, However, SE calculation is still widely used for comparison, such as varying aperture size, number, and/or spacing.
CONCLUSION
We discussed SE for different apertures of BLS by means of reverberation chamber testing, the SE between different apertures varies a lot, we see that the main factor is the hole dimension, and the shape (round or slot), hole numbers also make effect on SE. Meanwhile, we analyzed the SE calculation compared to the measurement, the data are proportional with the measurement result in the whole frequency although they are some dis-matched points, however, as the equation for SE calculation ignores some factors such as the variation of wave impedance, as well as the antenna direction and polarization, we don’t suggest to do SE calculation for complicated aperture evaluation, but it is still reasonable for us to use the SE calculation tool to do comparison especially for far-field immunity concern.
REFERENCES
[1] MIL-STD 285, Method of attenuation measurements for Electromagnetic Shielding Enclosures for Electronic Purposes, (1956)
[2] Wojciech J. KRZYSZTOFIK, Robert BOROWIEC, Bartosz BIEDA, Some Consideration on Shielding Effectiveness Testing by means of the Nested Reverberation Chambers.
[3] C.L. Holloway, D. A. Hill, M. Sandroni, J.M. Ladbury, J.Coder, G. Koepke, A.C. Marvin, Y.He “Use of Reverberation Chambers to Determine the Shielding Effectiveness of Physically Small, Electrically Large Enclosures and Cavities.” IEEE Transactions on Electromagnetic Compatibility. (2008).
[4] Frank B.J. Leferink, Hans Bergsma, Wim C. van Etten “Shielding Effectiveness Measurements using a Reverberation Chamber.”
[5] Martin Paul Robinson, Trevor M. Benson, Christos Christopoulos, John F. Dawson,
M. D. Ganley, A. C. Marvin, S. J. Porter, and David W. P. Thomas, “Shielding Effectiveness Measurements using a Reverberation Chamber.”