Author
Mekonen W. Buzuayene
Introduction
Changes to EMC standards that have taken place in recent years have had a significant impact on the costs associated with compliance testing. Testing to these revised EMC standards, in effect within the European Community, is a vital step to having the vital CE mark affixed to a product so that it can be sold throughout Europe. Specifically, there have been changes to EN 61326-1: 2006 and EN 61000-4-3: 2006. EN6326-1 is the European Union’s EMC standard for electrical equipment for measurement, control, and laboratory equipment. EN61000-4-3 details the immunity requirements of electrical and electronic equipment to radiated electromagnetic energy and includes the required testing and measurement techniques.
Frequencies: The Upward Trend
Key factors that can influence the process of compliance testing are: frequency range, sweep rate, frequency dwell time, modulation, field intensity, and field area calibration.
For EN61000-4-3 changes have been made in terms of frequency extension, field calibration, and dwell time. Its maximum frequency sweep rate has been reduced to one percent step size with a minimum dwell time of less than 0.5 seconds. EN61326-1:2006, Clause 6.2 now includes an upper testing frequency of 2.7 GHz (as compared to 1 GHz in the earlier version).1

Figure 1 shows the steady upward progression of frequency testing requirements—a situation brought about by the ever-expanding technologies of wireless voice and data transmission. This trend clearly indicates the need for reliable, robust product design that will withstand today’s EMI threats and those of tomorrow as well. To that end, high frequency testing is vital for protecting products from these ever-burgeoning threats.
Calculating the Number of Frequency Steps
Applying the 1 percent step size and assuming f0 is the start frequency, we write the first equation corresponding to number of steps (n). The frequency fn is expressed as:
fn = (1+1%)n *f0 (1)
For a decade:
fn = 10f0 (2)
By linking equation (1) and (2) we solve for n:
1.01n f0 = 10f0 (3)
However, to solve for n, one needs to convert the linear equation into logarithmic form by applying Log to each side of the equation. In essence, we are dealing in terms of Bels:
Log (1.01n) = Log (10) (4)
A Bels equation is a means of comparing two values or measurements such as powers or two voltages. Note that its unit changes to decibel (dB) from Bels (a smaller unit) when the equation is multiplied by 10. Rearranging and solving for n:
n*Log (1.01) = Log (10) (5)
n = Log (10) / Log (1.01) (6)
Equation 6 is nothing but a simple scalar in which its value (231.41 or 232) represents the number of steps in a decade.
Determining the Number of Decades
Next, we need to determine the number of decades within the frequency range (80 – 2700 MHz). To do that, we use the log of their ratio:
Decade = Log (fn/fo) (7)
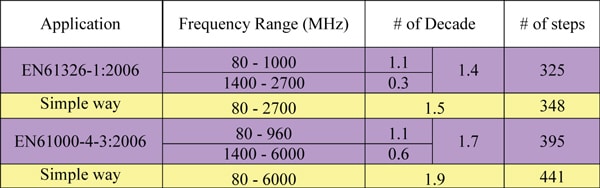
Plugging in the current standard test frequency range, (1000/80), into equation 7 comes to 1.1 decades. In other words, to complete a scan from 80 MHz to 1000 MHz, it requires 255 steps (x). Likewise, inserting 2700/80 in equation 7 for the new standard amounts to 1.5 decades or 348 steps. These figures indicate an increase of 36 percent over the original number of steps per decade and will have an negative impact on the overall testing time window. Table 1 shows the decade factor for various frequency test arrangements.

Note: Current under requirement column refers to EN6100-4-3:1996; Future-1 refers to EN61326-1:2006; and Future-2 refers to EN61000-4-3:2006.
Length of Sweep Time
How long does it take to run a sweep? To find out how long it will take to sweep from 80 to 1000 MHz, one must multiply the number of decades by the rate of the sweep and then covert that result to minutes. According to the radiated immunity standard, the sweep rate should not exceed 1.5 x 10–3 decades per second, or 1 decade in 666.67 seconds.
Using the same formula with the 1.5 decade figure plugged in results in 17 minutes of testing time—thereby increasing sweep time by 33%. The import of these calculations is that if it took eight hours to complete product testing under the previous standard, it will take about eleven hours using new one.
Assuming that there are four sides (very common) to the device under test and that two antenna scans (horizontal and vertical polarization) are needed for each side, a total of eight scans will be required to complete the test. Time wise, it will take about 2.5 hours to carry out radiated immunity testing, and this estimation does not take into account the time spent on test setup and uploads of needed software.
Also, control software will take a finite time to settle at each frequency as it progresses toward the required level of forward power. Normally, it drops the power, changes frequency, allows time for the signal generator to settle (under one second), turns on the modulation, loads up a new calibration file, and then increases the output level until the required forward power is reached. All these steps easily amount to two or three seconds at each frequency step—easily amounting to 12 minutes per scan.
Additionally, there will be a delay (depending on how active the test engineer is) as the amplifiers /antennas are switched at 200 – 300 MHz or at other applicable frequencies. The time needed for this activity will total about 30 to 40 minutes per side, without adding the time needed between each scan to rotate the product. The final figure for a completing a full test on all four sides comes to be about five hours.
Comparison
Of course, most testers would argue that they would opt for the simplest test routine. Complicating matters, the frequencies covered by EN61326-1:2006 and EN61000-4-3:2006 vary by magnitude. The table below indicates the consequent number of steps for each test option chosen and is indicative of rising test costs.
One comment here is that the cost per hour of testing is subjective to local pricing and will differ from region to region. The $300/hour rate used in Table 3 is used as an example of the typical hourly testing rate in Bay Area of Northern California.

Conclusion
An appropriate mathematical model (basically by employing a Bel equation) clearly demonstrates the time and financial consequences of complying with the revised editions of EN61326 and/or EN61000-4-3. As table 4 shows, the cost of testing can easily increase from between 26 and 71 percent depending on which compliance method is chosen. This increased expense should be factored in when scheduling laboratory testing time. Electronics manufacturers must be aware that the new standards not only impose more stringent design constraints but also add a considerable financial burden when carrying out crucial compliance testing.
Resources
[1] EN61326-1:2006, Clause 6.2, Tables 1-3, pp. 11–14.
[2] EN61000-4-3:2006, Clause 8, p. 20.







