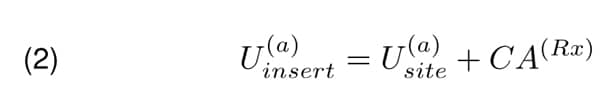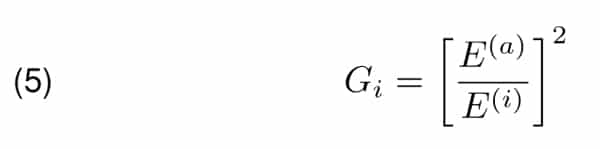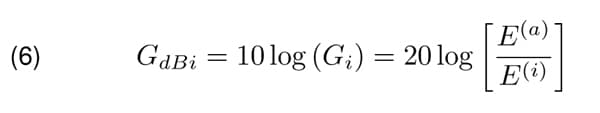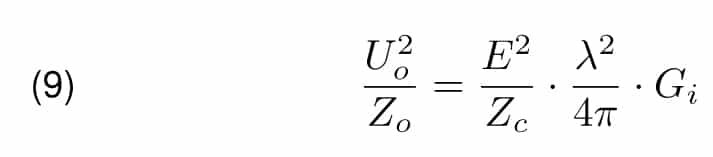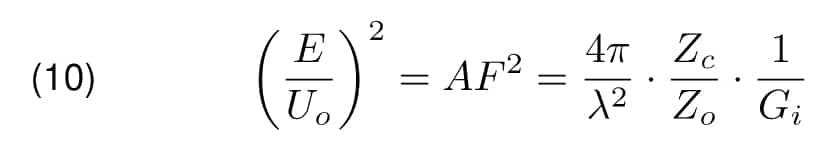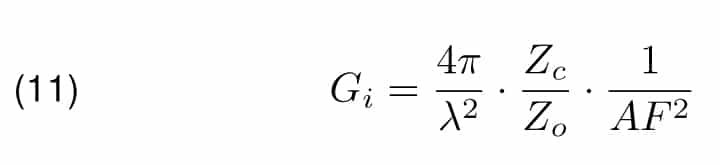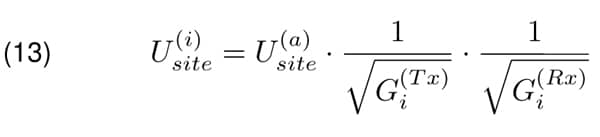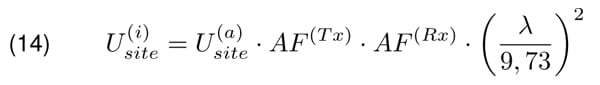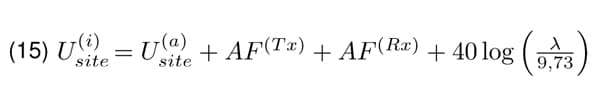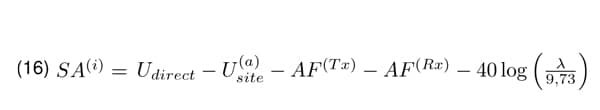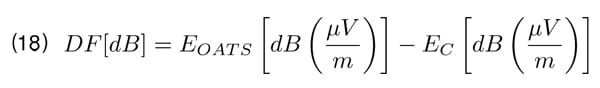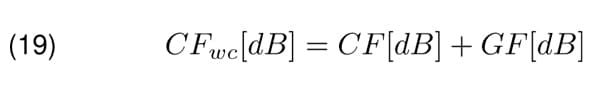Note: This article has been translated from Polish to English. It can be found in its original language in the 2014 Europe EMC Guide.
Jan Sroka, Professor, Warsaw University of Technology, Warsaw, Poland
ABSTRACT
The term “site attenuation” is used in the theory of electromagnetic fields as extension of the term “attenuation,” which is well known in circuit theory. The site attenuation depends on the antennas being used. Therefore, it is not an objective indicator in the evaluation of test sites such as semi-anechoic chambers (SAC) and open area test sites (OATS) intended for radiated emission measurements. The so-called normalized site attenuation NSA is defined as such an indicator [2]. This is the site attenuation “measured” with the isotropic antennas and modified thereafter with the compensation of the term dependent on the wave length, the intrinsic and the matching impedances. Such site attenuation is not measurable but it can be derived from the measurements with any other antennas’ set. The test site conforms with requirements of [2] if the measured NSA does not deviate more than ±4dB from the theoretical one. Chambers with |∆N SASAC | > 4dB can still be used for testing, provided they have the chamber factor (CF) and the gray factor (GF) measured. The first one is the expected value and can be used for correction. The second is the maximal error and can be used in the measurement uncertainty budget.
Keywords: normalized site attenuation, semi-anechoic chamber, isotropic antenna, chamber factor, gray factor.
INTRODUCTION
The halt infinite vacuum with a perfectly reflecting floor is used as the reference environment for verification of the semi-anechoic chambers (SAC) and the open area test sites (OATS) intended for radiated emission measurements in the frequency range from 30MHz to 1GHz. As the reference quantity, the normalized site attenuation (NSA) is applied. The NSA is “measured” with a set of isotropic antennas—it is not measurable, but the relation between the NSA and the site attenuation measured with any other set of antennas can be derived. The test site conforms with requirements of [2] if the measured NSA does not deviate more than ±4dB from the theoretical one.
There exist chambers, particularly old ones, in which NSA deviates more then ±4dB from the theoretical one. Absorber materials (i.e. ferrites), which efficiently attenuate magnetic field in the frequency range from 30M Hz to about 200 MHz, have been available only for past few years. Chambers with |∆N SASAC| < ±12dB can still be used for testing, provided they have measured the chamber factor CF and the gray factor GF [3], [6].
A big deviation of the NSA from the theoretical value means that by testing the receiving antenna is not in the far field zone of the EUT.
NORMALIZED SITE ATTENUATION (NSA)
The semi-anechoic chamber or the open area test site with antennas’ set used by NSA measurement: transmitting T x and receiving Rx can be considered as the two-port by which the feeding point of the transmitting antenna is the input port and the feeding point of the receiving antenna is the output port. Attenuation of such a two-port is called site attenuation SA.
For SA measurements following equipment must be used: the C W signal generator with signal level Ug, the cable of the transmitting antenna with attenuation C A(T x), the cable of the receiving antenna with attenuation C A(Rx) and the measurement receiver. The measurement is performed in two steps. In the first reference voltage Uref at the connecting point to the receiving antenna with removed antennas as shown in Figure 1 is measured. This signal is related to the signal measured by the receiver Udirect in dB scale as follows:
In the next step antennas are mounted and voltage U(a)insert in the feeding point of the receiving antenna with “inserted” two-port as shown in Figure 2 is measured. This signal is related to the signal measured by the receiver U(a)site in dB scale as follows:
According to the definition of attenuation [7], the difference of Equations 1 and 2 is the site attenuation SA.
This attenuation1 is independent on the cables’ attenuations but dependent on antennas used2. That’s why it is useless in evaluation of the test sites. Only site attenuation verified always and everywhere with the same set of antennas can serve for conformity validation. Isotropic lossless antennas are chosen in [2] for this aim.
An isotropic antenna is an artificial entity. It cannot be built, but the site attenuation expressed with Equation 3 can be recalculated to the site attenuation that would be measured with isotropic antennas (Equation 4). For this recalculation the terms such as energetic antenna gain G, named also antenna gain, antenna’s effective aperture Ae and antenna factor AF [4], [8] are needed.
The antenna gain is the quotient of the power density in the far field zone in direction of the biggest radiation of the antenna to the power density of the lossless isotropic antenna, if in both cases the forward power in the antenna’s feeding point is the same. Denoting the power density with the Poynting vector, applying the relation between modules of the electric field and magnetic field vectors E and H in the far field zone yields relation between the antenna gain and modules of electrical fields of both antennas E(a) , E(i).
In dB scale, Equation 5 yields:
The symbol dBi is used in order to emphasize the isotropic antenna as the reference.
Let’s imagine the receiving antenna placed in uniform filed with electric field intensity E such that antenna and field are matched in respect to polarization3 . Let’s denote the power delivered to the matched load i.e. power available in the field, which is captured by the receiving antenna and converted in the matched load, with the symbol Po. The area from which the receiving antenna must extract the field in order to deliver power Po to the load is called the antenna’s effective aperture Ae
where Zc is intrinsic site impedance.
Effective aperture of the isotropic antenna can be expressed as follows Ae = λ, where λ denotes the wavelength.
Let’s again imagine the receiving antenna placed in uniform filled with electric field intensity E such that antenna and field are matched. IF the signal receiver with matched impedance mounted in the antenna feeding point measures signal Uo, then the quotient of E and Uo is called the antenna factor AF.
In dB scale AF is expressed with [dB(1/m)].
In order to derive relation between the antenna factor AF and the antenna gain G let’s again imagine the receiving antenna placed in uniform field with electric field intensity E such that antenna and field are matched. Power dissipated in the matched impedance Zo mounted on the antenna feeding point is equal to U2 /Zo . On the other side it is power captured with the antenna i.e. it is product of the Poynting vector, effective aperture and antenna gain
or rearranged
finally
For further consideration following rearrangement of Equation 11 for vacuum in which Zo = 120πΩ and matched load equal to Zo = 50Ω is useful
Let’s assume that isotropic antennas are used by the measurement of the site attenuation. The field in the far zone radiated by the transmitting antenna, according to Equation 5, would be G(T x) times smaller. Moreover, according to the definition of the antenna gain, the receiving antenna would be able to extract G(Rx) times less power. Finally, signal measured with the receiver U(i)site would be Gi x Gi(Rx) times smaller.
By setting Equation 12 in the last formula, the final result can be obtained.
or in dB scale
Setting this relation to Equation 4, the formula for site attenuation measured with isotropic antennas can be obtained.
In the document [2], the normalized site attenuation is defined as it would be measured with isotropic antennas, Equation 16 and modified thereafter such that the term 40 log λ disappears. Therefore
Unit of N SA in the dB scale is [dB(m2 )].
In the second step of the measurement of the site atten- uation position the transmitting antenna coincides with the EU T position and receiving antenna is in the same place as the receiving antenna by testing. The height of the transmitting antenna is kept constant 1m over the floor and height of the receiving antenna is changed from 1m to 4m and maximal signal is registered and used for calculation as U(a)
Measurement is performed for two antennas’ polarization: horizontal and vertical in respect to the floor. Biconical wide band antennas or dipole antennas with changeable arms’ length are used. By verification of the 3m test site and by using dipole antennas with changeable arms’ length Equation 17 must be corrected with coefficients listed in the table in [2].
For the open area test site N SA is measured only in one direction. In the semi anechoic chamber N SA is measured for the so called EU T volume. It is the gauge with the shape of the vertical cylinder enveloping the EU T including connected cables. The transmitting antenna is usually placed in five position: in the center of the cylinder and four positions on the outer surface.
According to the document [2] SAC or OAT S is con- form if the measured N SA does not deviate from the theoretical one about no more than ±4dB (|∆N SA| ≤ 4dB). This deviation cannot be compensated in the measurement but must be built into the uncertainty budget.
Dominant source of uncertainty by the measurement ac- cording to Equation 17 are uncertainties of the antennas’ factors AF(T x) and AF(Rx).
CHAMBER FACTOR AND GRAY FACTOR
In a semi-anechoic chamber with 3m test site the receiving antenna is situated in the near field zone of the EU T by the frequencies starting from 30M H z. N SA is measured with the electric field antennas. Therefore it does not imply information about magnetic field generated by the EU T in the near field. The chamber factor and gray factor do it.
For determination of the chamber factor electric field in- side the EU T volume must be measured in the similar way as by the N SA measurements, but with four principal differences:
- field is generated with the wide band comb generator instead of the C W signal generator,
- magnetic loop antenna in addition to electric dipole an- tenna is used for transmission,
- the good quality open area test site serves as the refer- ence,
- the receiving antenna is the wide band electric antenna.
For each position of the transmitting antenna, for both polarizations and both kinds of antenna electric field EC is measured with the receiving antenna. Next, the chamber deviation factor DF is calculated as follows:
in which EOAT S is the electric field measured in the same circumstances in the reference open area test site.
If validation is done by five antenna positions, twenty frequency dependent deviation factors are measured. In the next step the upper and lower envelope of DF is calculated separately for each polarization.
Chamber factor C F is frequency and polarization de- pendent arithmetic mean value of the upper and lower envelopes of the deviation factor DF. The gray factor GF is frequency and polarization dependent distance between the chamber factor C F and the upper or lower envelope of the deviation factor DF .
Document [3] suggests to apply the chamber factor C F alternatively. Either to treat it as the expected value and apply it as the correction by the EU T testing4 or to determine the worst case chamber factor C Fwc for each frequency and polarization as follows
and use it for correction of the the measurement result by the EU T testing.
Approach with the worst case chamber factor C Fwc is an handicap but it ensures the measurement results by the EU T testing not to be smaller than measured in the site conform with the [2] requirements.
The gray factor GF is used as the maximal error with uniform distribution because there is the same probability the true value to be situated somewhere between the envelopes.
The chamber can be used for the EU T measurements if C F is between ±10dB and the gray factor GF is less than 5dB.
CONCLUSION
The formula derived in the paper for the normalized site attenuation explains the term “normalized”. It consists in determination of the site attenuation always and everywhere with the set of isotropic antennas.
The semi anechoic chambers which do not fulfill the requirement |∆N SASAC | ≤ 4dB can be despite this used for radiated emission measurements if they have the chamber factor C F and the gray factor GF measured. The first one is used as the correction, the second as the maximal error.
FOOTNOTES
1Notice that Equation 3 denotes the attenuation and therefore it is independent on the impedance mismatching in feeding points of the antennas, provide the signal generator, measurement receiver and cables are matched to the reference impedance which is usually 50Ω resistance. Otherwise Equation 3 is the site insertion loss [7], which depends on antennas impedance mismatching.
2Antennas constitute the interior of the the two-port. Ability of the transmitting antenna to convert the guided wave to the radiated field and ability of the reverse conversion by the receiving antenna are individual antennas attributes which determine measured site attenuation. Therefore upper case (a) in the site attenuation symbol
3Polarization matching means such antenna orientation, that signal induced in the antenna is maximal. In case of the dipole antenna the arms of the antenna are parallel to the lines of the electric field.
4C F for some frequencies can be negative in dB scale. It means overestimated measurement result in respect to the conform test site.
REFERENCES
[1] A. Askri, C. Vollaire, L. Nicolas, D. Prebet: Normalized Site Attenuation Standard Correction From Numerical Computing. IEEE Trans. on Magnetics, Vol. 38, No.2, March 2002.
[2] CISPR 16-1-4:2004 + A1:2005 + A2:2005: Specifi- cation for radio disturbance and immunity measuring apparatus and methods – Part 1-4: Radio disturbance and immunity measuring apparatus – Ancilliary equip- ment – Radiated disturbances. IEC, 2005.
[3] CENELEC R110-003: Guidelines on how to use ane- choic enclosures that do not fulfill the requirements re- garding normalized site attenuation for pre-compliance tests of products. CENELEC, 1995.
[4] http.//www.antenna-theory.com/definitions
[5] IEC 60050-International Electrotechnical Vocabulary, www.electropedia.org
[6] I. H. Hubing: Correcting radiated emission data mea- sured in nonideal environments. IEEE Trans. EMC, Vol. EMC-28, No.2, May 1986.
[7] J. Sroka, Niepewnos´ c´ pomiarowa w badaniach EMC, pomiary emisyjnos´ ci radioelektrycznej . OWPW, Warszawa, 2009.
[8] J. Szóstka: Fale i anteny. WKŁ, Warszawa 2006.
ABOUT THE AUTHOR
Professor Jan Sroka is with the Warsaw University of Technology, Koszykowa 75, 00-662 Warszawa, e- mail: (J.Sroka@iem.pw.edu.pl) and the EMC-Testcenter AG, Mossäckerstr. 77, CH-8105 Regensdorf, Switzerland, e-mail: (jsroka@emc-testcenter.com). He is also the EMC expert by the company ASTAT Sp. z o. o. Poznan´ (www.astat.com.pl).